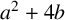Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gaál, István
2024.
Monogenity and Power Integral Bases: Recent Developments.
Axioms,
Vol. 13,
Issue. 7,
p.
429.
Benfield, Brennan
and
Lippard, Oliver
2025.
Connecting Zeros in Pisano Periods to Prime Factors of
K
-Fibonacci Numbers
.
The Fibonacci Quarterly,
Vol. 63,
Issue. 2,
p.
240.
Benfield, Brennan
and
Lippard, Oliver
2025.
Fixed Points of
K
-Fibonacci Sequences
.
The Fibonacci Quarterly,
Vol. 63,
Issue. 2,
p.
259.