Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T05:51:40.519Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON GROUPS WHOSE PROPER LARGE SUBGROUPS HAVE A TRANSITIVE NORMALITY RELATION

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  04 November 2016

FRANCESCO DE GIOVANNI  and
MARCO TROMBETTI
FRANCESCO DE GIOVANNI*
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, Napoli, Italy email degiovan@unina.it
MARCO TROMBETTI
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, Napoli, Italy email marco.trombetti@unina.it
*
✉ degiovan@unina.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A group 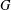$G$ is said to have the 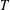$T$ -property (or to be a 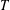$T$ -group) if all its subnormal subgroups are normal, that is, if normality in 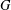$G$ is a transitive relation. The aim of this paper is to investigate the behaviour of uncountable groups of cardinality  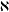$\aleph$ whose proper subgroups of cardinality 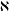$\aleph$ have a transitive normality relation. It is proved that such a group  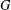$G$ is a 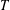$T$ -group (and all its subgroups have the same property) provided that 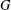$G$ has an ascending subnormal series with abelian factors. Moreover, it is shown that if 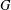$G$ is an uncountable soluble group of cardinality 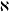$\aleph$ whose proper normal subgroups of cardinality  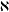$\aleph$ have the 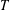$T$ -property, then every subnormal subgroup of 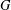$G$ has only finitely many conjugates.

Keywords

uncountable groupT-groupT -group

MSC classification

Primary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 38 - 47
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Casolo, C., ‘Groups with finite conjugacy classes of subnormal subgroups’, Rend. Semin. Mat. Univ. Padova 81 (1989), 107–149.Google Scholar
De Falco, M. and de Giovanni, F., ‘Groups with many subgroups having a transitive normality relation’, Bol. Soc. Brasil. Mat. 31 (2000), 73–80.Google Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Groups whose proper subgroups of infinite rank have a transitive normality relation’, Mediterr. J. Math. 10 (2013), 1999–2006.Google Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Large soluble groups and the control of embedding properties’, Ric. Mat. 63(supplement) (2014), 117–130.CrossRefGoogle Scholar
Gaschütz, W., ‘Gruppen in denen das Normalteilersein transitiv ist’, J. reine angew. Math. 198 (1957), 87–92.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Uncountable groups with restrictions on subgroups of large cardinality’, J. Algebra 447 (2016), 383–396.CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M., ‘Nilpotency in uncountable groups’, J. Aust. Math. Soc., to appear.Google Scholar
de Giovanni, F. and Trombetti, M., ‘A note on uncountable groups with modular subgroup lattice’, Arch. Math. (Basel) (2016), doi:10.1007/s00013-016-0964-5.CrossRefGoogle Scholar
Obraztsov, V. N., ‘An embedding theorem for groups and its corollaries’, Math. USSR-Sb. 66 (1990), 541–553.CrossRefGoogle Scholar
Robinson, D. J. S., ‘Groups in which normality is a transitive relation’, Proc. Cambridge Philos. Soc. 60 (1964), 21–38.Google Scholar
Robinson, D. J. S., ‘Groups which are minimal with respect to normality being intransitive’, Pacific J. Math. 31 (1969), 777–785.CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).CrossRefGoogle Scholar
Robinson, D. J. S., ‘The vanishing of certain homology and cohomology groups’, J. Pure Appl. Algebra 7 (1976), 145–167.Google Scholar
Robinson, D. J. S., ‘Splitting theorems for infinite groups’, Sympos. Math. 17 (1976), 441–470.Google Scholar
Shelah, S., ‘On a problem of Kurosh, Jónsson groups, and applications’, in: Word Problems II—The Oxford Book (North-Holland, Amsterdam, 1980), 373–394.CrossRefGoogle Scholar