Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T05:02:48.773Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES

Part of: Diophantine equations Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  21 October 2020

YASUTSUGU FUJITA Open the ORCID record for YASUTSUGU FUJITA [Opens in a new window]  and
MAOHUA LE Open the ORCID record for MAOHUA LE [Opens in a new window]
YASUTSUGU FUJITA*
Affiliation:
Department of Mathematics, College of Industrial Technology, Nihon University, 2-11-1 Shin-ei, Narashino, Chiba, Japan
MAOHUA LE
Affiliation:
Institute of Mathematics, Lingnan Normal College, Zhangjiang, Guangdong, 524048, China e-mail: lemaohua2008@163.com
*
e-mail: fujita.yasutsugu@nihon-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Jeśmanowicz conjectured that 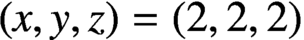$(x,y,z)=(2,2,2)$ is the only positive integer solution of the equation 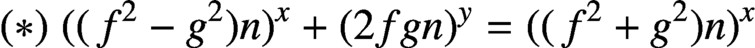$(*)\; ((\kern1.5pt f^2-g^2)n)^x+(2fgn)^y=((\kern1.5pt f^2+g^2)n)^x$ , where n is a positive integer and f, g are positive integers such that 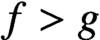$f>g$ 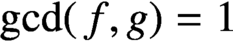, $\gcd (\kern1.5pt f,g)=1$ and 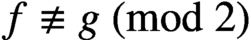$f \not \equiv g\pmod 2$ . Using Baker’s method, we prove that: (i) if 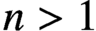$n>1$ 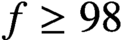, $f \ge 98$ and 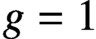$g=1$ , then $(*)$ has no positive integer solutions 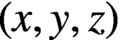$(x,y,z)$ with 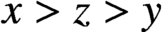$x>z>y$ ; and (ii) if 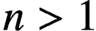$n>1$ 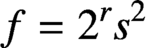, $f=2^rs^2$ and 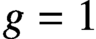$g=1$ , where r, s are positive integers satisfying 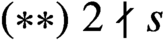$(**)\; 2 \nmid s$ and 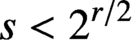$s<2^{r/2}$ , then $(*)$ has no positive integer solutions 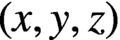$(x,y,z)$ with 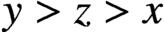$y>z>x$ . Thus, Jeśmanowicz’ conjecture is true if 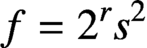$f=2^rs^2$ and 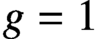$g=1$ , where r, s are positive integers satisfying $(**)$ .

Keywords

Jeśmanowicz’ conjecturePythagorean tripleternary purely exponential Diophantine equation

MSC classification

Primary: 11D61: Exponential equations
Secondary: 11J86: Linear forms in logarithms; Baker's method
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 29 - 39
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bennett, M. A., Ellenberg, J. S. and Ng, N. C., ‘The Diophantine equation ${A}^4+{2}^{\delta }{B}^2={C}^n$ ’, Int. J. Number Theory 6 (2010), 311–338.CrossRefGoogle Scholar
Jeśmanowicz, L., ‘Several remarks on Pythagorean numbers’, Wiad. Mat. 1 (1955/1956), 196–202 (in Polish).Google Scholar
Laurent, M., ‘Linear forms in two logarithms and interpolation determinants II’, Acta Arith. 133 (2008), 325–348.CrossRefGoogle Scholar
Le, M.-H., ‘A note on Jeśmanowicz’ conjecture concerning Pythagorean triples’, Bull. Aust. Math. Soc. 59 (1999), 477–480.CrossRefGoogle Scholar
Le, M.-H., Scott, R. and Styer, R., ‘A survey on the ternary purely exponential Diophantine equation ${a}^x+{b}^y={c}^z$ ’, Surv. Math. Appl. 14 (2019), 109–140.Google Scholar
Lu, W.-D., ‘On the Pythagorean numbers $4{n}^2-1$ , $4n$ and $4{n}^2+1$ ’, J. Sichuan Univ. Nat. Sci. Ed. 5 (1959), 39–42 (in Chinese).Google Scholar
Miyazaki, T., ‘A remark on Jeśmanowicz’ conjecture for the non-coprimality case’, Acta Math. Sin. Engl. Ser. 31 (2015), 1255–1260.CrossRefGoogle Scholar
Mordell, L. J., Diophantine Equations (Academic Press, London, 1969).Google Scholar
Yang, H. and Fu, R.-Q., ‘A note on Jeśmanowicz’ conjecture concerning primitive Pythagorean triples’, J. Number Theory 156 (2015), 183–194.CrossRefGoogle Scholar
Zhang, X.-W. and Zhang, W.-P., ‘The exponential Diophantine equation ${(({2}^{2m}-1)n)}^x+{({2}^{m+1}n)}^y={(({2}^{2m}+1)n)}^z$ ’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 57 (2014), 337–344.Google Scholar