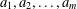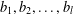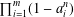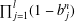Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mehraban, Elahe
Gulliver, T. Aaron
and
Hincal, Evren
2025.
An RSA cryptosystem based on Lehmer sequences in Some classes of groups.
Advances in Mathematics of Communications,
Vol. 19,
Issue. 4,
p.
1026.
Mehraban, Elahe
Gulliver, T. Aaron
and
Hinçal, Evren
2025.
New signature schemes from the Hadamard-type <inline-formula><tex-math id="M1">$ (k,t)- $</tex-math></inline-formula>generalized Jacobsthal-Lehmer sequences on the <inline-formula><tex-math id="M2">$ 2- $</tex-math></inline-formula>generator <inline-formula><tex-math id="M3">$ p- $</tex-math></inline-formula>group of nilpotency class <inline-formula><tex-math id="M4">$ 2 $</tex-math></inline-formula>.
Advances in Mathematics of Communications,
Vol. 19,
Issue. 6,
p.
1657.