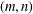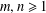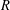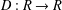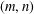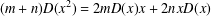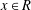Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
An, Guang Yu
and
He, Jun
2019.
Characterizations of (m,n)-Jordan Derivations and (m,n)-Jordan Derivable Mappings on Some Algebras.
Acta Mathematica Sinica, English Series,
Vol. 35,
Issue. 3,
p.
378.
Bennis, Driss
Dhara, Basudeb
and
Fahid, Brahim
2021.
More on the Generalized (m,n)-Jordan Derivations and Centralizers on Certain Semiprime Rings.
Bulletin of the Iranian Mathematical Society,
Vol. 47,
Issue. 1,
p.
217.