Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McCaughan, D. J.
and
McDougall, D.
1977.
Criteria for subnormality.
Archiv der Mathematik,
Vol. 29,
Issue. 1,
p.
451.
Kawamoto, Naoki
1979.
Subideality and ascendancy in generalized solvable Lie algebras.
Hiroshima Mathematical Journal,
Vol. 9,
Issue. 3,
Wehrfritz, B.A.F.
1980.
Wielandt's subnormality criterion and linear groups.
Journal of Algebra,
Vol. 67,
Issue. 2,
p.
491.
Whitehead, Jennifer
1980.
Subnormality and ascendancy in soluble groups of finite rank.
Archiv der Mathematik,
Vol. 34,
Issue. 1,
p.
10.
Tôgô, Shigeaki
1980.
Subnormality and ascendancy in groups.
Hiroshima Mathematical Journal,
Vol. 10,
Issue. 3,
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.
Kawamoto, Naoki
1983.
Finitely generated subalgebras of generalized solvable Lie algebras.
Hiroshima Mathematical Journal,
Vol. 13,
Issue. 1,
Aldosray, Falih A. M.
1984.
Subideals and ascendant subalgebras of Lie algebras.
Archiv der Mathematik,
Vol. 42,
Issue. 6,
p.
520.
Kondrat'ev, A. S.
Makhnev, A. A.
and
Starostin, A. I.
1989.
Finite groups.
Journal of Soviet Mathematics,
Vol. 44,
Issue. 3,
p.
237.
BARREIROS, L.P.
and
CASTILLO, P.F. ARCE
2017.
ANÁLISE DA ABORDAGEM GAMMA-PHI NA MODELAGEM TERMODINÂMICA DE SISTEMAS BINÁRIOS CONTENDO COMPONENTES PRESENTES NO BIODIESEL.
p.
692.
Goka, Tomotsugu
and
Lee, Chanwoo
2018.
The establishment and development process of Dai Nippon Kyudo Kai and its organizational forms..
Taiikugaku kenkyu (Japan Journal of Physical Education, Health and Sport Sciences),
Vol. 63,
Issue. 1,
p.
121.
Dhamodharan, Duraisami
Ghoderao, Pradnya NP
Park, Cheol-Woong
and
Byun, Hun-Soo
2022.
Bubble and dew-point measurement of mixtures of 1H,1H,2H-perfluoro-1-octene and 1H,1H,2H,2H-perfluoro-1-octanol in supercritical CO2.
New Journal of Chemistry,
Vol. 46,
Issue. 15,
p.
7271.


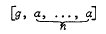 lies in
lies in 