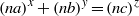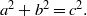Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tang, Min
and
Weng, Jian-Xin
2014.
JEŚMANOWICZ' CONJECTURE WITH FERMAT NUMBERS.
Taiwanese Journal of Mathematics,
Vol. 18,
Issue. 3,
MA, MI-MI
and
WU, JIAN-DONG
2015.
ON THE DIOPHANTINE EQUATION (an)x+ (bn)y= (cn)z.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 4,
p.
1133.
Yang, Hai
and
Fu, Ruiqin
2015.
A note on Jeśmanowicz' conjecture concerning primitive Pythagorean triples.
Journal of Number Theory,
Vol. 156,
Issue. ,
p.
183.
Miyazaki, Takafumi
2015.
A remark on Jeśmanowicz’ conjecture for the non-coprimality case.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 8,
p.
1255.
Tingting, Wang
Xiaonan, Wang
and
Yingzhao, Jiang
2018.
An application of the Baker method to Jeśmanowicz’ conjecture on Pythagorean triples.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 112,
Issue. 2,
p.
385.
Feng, Cheng
and
Luo, Jiagui
2022.
On the exponential Diophantine equation $ \left(\frac{q^{2l}-p^{2k}}{2}n\right)^x+(p^kq^ln)^y = \left(\frac{q^{2l}+p^{2k}}{2}n\right)^z $.
AIMS Mathematics,
Vol. 7,
Issue. 5,
p.
8609.
Dong, Ziyu
and
Zhao, Zhengjun
2023.
An application of $ p $-adic Baker method to a special case of Jeśmanowicz' conjecture.
AIMS Mathematics,
Vol. 8,
Issue. 5,
p.
11617.
黄, 日娣
2023.
On the Diophantine Equation (75n)<sup>x</sup>+ (308n)<sup>y</sup>= (317n)<sup>z</sup>.
Pure Mathematics,
Vol. 13,
Issue. 11,
p.
3358.
Kitayama, Hidetaka
Tagawa, Hiroyuki
and
Urahashi, Keiichi
2023.
Jeśmanowicz’ conjecture for non-primitive Pythagorean triples.
Periodica Mathematica Hungarica,
Vol. 86,
Issue. 2,
p.
442.
Fan, Nan
and
Luo, Jiagui
2023.
On the conjecture of Je$ \acute{\textbf{s}} $manowicz.
AIMS Mathematics,
Vol. 8,
Issue. 6,
p.
14232.