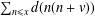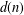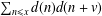Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ye, Dongxi
2021.
A remark on the average number of divisors of a quadratic polynomial.
Archiv der Mathematik,
Vol. 116,
Issue. 1,
p.
49.