Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T22:01:43.218Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE POLIGNAC NUMBERS

Part of: Additive number theory; partitions Elementary number theory

Published online by Cambridge University Press:  13 March 2014

HAO PAN
HAO PAN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China email haopan1979@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 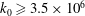$k_0\geq 3.5\times 10^6$ and 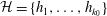$\mathcal{H}=\{h_1,\ldots,h_{k_0}\}$ is admissible. Then, for any 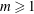$m\geq 1$, the set 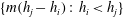$\{m(h_j-h_i):\, h_i<h_j\}$ contains at least one Polignac number.

Keywords

Polignac numberadmissible set

MSC classification

Secondary: 11P32: Goldbach-type theorems; other additive questions involving primes 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 500 - 502
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Motohashi, Y. and Pintz, J., ‘A smoothed GPY sieve’, Bull. Lond. Math. Soc. 40 (2008), 298–310.CrossRefGoogle Scholar
Pintz, J., ‘Polignac numbers, conjectures of Erdős on gaps between primes, arithmetic progressions in primes, and the bounded gap conjecture’, Preprint, arXiv:1305.6289.Google Scholar
de Polignac, A., ‘Six propositions arithmologiques déduites du crible d’Ératosthène’, Nouv. Ann. Math. 8 (1849), 423–429.Google Scholar
Zhang, Y., ‘Bounded gaps between primes’, Ann. of Math. (2), to appear.Google Scholar