Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T03:46:04.557Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE SUM OF RECIPROCALS

Part of: Combinatorics Sequences and sets Elementary number theory

Published online by Cambridge University Press:  17 May 2019

YUCHEN DING  and
YU-CHEN SUN Open the ORCID record for YU-CHEN SUN [Opens in a new window]
YUCHEN DING
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China email 840172236@qq.com
YU-CHEN SUN*
Affiliation:
Medical School, Nanjing University, Nanjing 210093, People’s Republic of China email syc@smail.nju.edu.cn
*
✉syc@smail.nju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that, given a positive integer 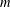$m$, there is a sequence 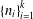$\{n_{i}\}_{i=1}^{k}$ of positive integers such that

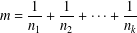$$\begin{eqnarray}m=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\cdots +\frac{1}{n_{k}}\end{eqnarray}$$
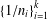with the property that partial sums of the series $\{1/n_{i}\}_{i=1}^{k}$ do not represent other integers.

Keywords

sum of reciprocalsEgyptian fractioncover of the integers

MSC classification

Primary: 11A05: Multiplicative structure; Euclidean algorithm; greatest common divisors
Secondary: 05A17: Partitions of integers 11A51: Factorization; primality 11B75: Other combinatorial number theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 189 - 193
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Berger, M. A., Felzenbaum, A. and Fraenkel, A. S., ‘Improvements to the Newman–Znám result for disjoint covering systems’, Acta Arith. 50 (1988), 1–13.Google Scholar
Chen, Y. G., ‘On integers of the forms k r - 2 n and k r 2 n + 1’, J. Number Theory 98 (2003), 310–319.Google Scholar
Erdős, P., ‘On integers of the form 2 k + p and some related problems’, Summa Brasil. Math. 2 (1950), 113–123.Google Scholar
Guo, S. and Sun, Z. W., ‘On odd covering systems with distinct moduli’, Adv. Appl. Math. 35 (2005), 182–187.Google Scholar
Pan, H. and Zhao, L. L., ‘Clique numbers of graphs and irreducible exact m-covers of the integers’, Adv. Appl. Math. 43 (2009), 24–30.10.1016/j.aam.2008.09.004Google Scholar
Porubský, Š., ‘Covering systems and generating functions’, Acta Arith. 26 (1974–1975), 223–231.Google Scholar
Porubský, Š., ‘On m times covering systems of congruences’, Acta Arith. 29 (1976), 159–169.10.4064/aa-29-2-159-169Google Scholar
Sun, Z. W., ‘On exactly m times covers’, Israel J. Math. 77 (1992), 345–348.Google Scholar
Sun, Z. W., ‘Covering the integers by arithmetic sequences’, Acta Arith. 72 (1995), 109–129.10.4064/aa-72-2-109-129Google Scholar
Sun, Z. W., ‘Covering the integers by arithmetic sequences II’, Trans. Amer. Math. Soc. 348 (1996), 4279–4320.Google Scholar
Sun, Z. W., ‘On integers not of the form ±pa ± qb ’, Proc. Amer. Math. Soc. 128 (2000), 997–1002.Google Scholar
Zhang, M. Z., ‘A note on covering systems of residue classes’, J. Sichuan Univ. (Nat. Sci. Ed.) 26 (1989), 185–188; Special Issue.Google Scholar
Zhang, M. Z., ‘On irreducible exactly m times covering system of residue classes’, J. Sichuan Normal Univ. Nat. Sci. Ed. 28 (1991), 403–408.Google Scholar