Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T10:37:58.510Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTES ON 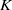$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS

Part of: Connections with other structures, applications Topological and differentiable algebraic systems

Published online by Cambridge University Press:  30 August 2012

HANFENG WANG  and
WEI HE
HANFENG WANG
Affiliation:
Institute of Mathematics, Nanjing Normal University, Nanjing 210046, PR China Department of Mathematics, Shandong Agricultural University, Taian 271018, PR China (email: whfeng@sdau.edu.cn)
WEI HE*
Affiliation:
Institute of Mathematics, Nanjing Normal University, Nanjing 210046, PR China (email: weihe@njnu.edu.cn)
*
✉For correspondence; e-mail: weihe@njnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, it is shown that there exists a connected topological group which is not homeomorphic to any 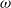$\omega $-narrow topological group, and also that there exists a zero-dimensional topological group 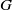$G$ with neutral element $e$ such that the subspace 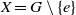$X = G\setminus \{e\}$ is not homeomorphic to any topological group. These two results give negative answers to two open problems in Arhangel’skii and Tkachenko [Topological Groups and Related Structures (Atlantis Press, Amsterdam, 2008)]. We show that if a compact topological group is a 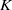$K$-space, then it is metrisable. This result gives an affirmative answer to a question posed by Malykhin and Tironi [‘Weakly Fréchet–Urysohn and Pytkeev spaces’, Topology Appl. 104 (2000), 181–190] in the category of topological groups. We also prove that a regular 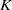$K$-space 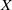$X$ is a weakly Fréchet–Urysohn space if and only if 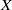$X$has countable tightness.

Keywords

$\omega $-narrow topological groupzero-dimensional topological group$\uppercase {k}$-spacecountable tightness

MSC classification

Secondary: 54H11: Topological groups 22A05: Structure of general topological groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 493 - 502
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Arhangel’skii, A. V. & Ponomarev, V. I., ‘On dyadic bicompacta’, Soviet. Math. Dokl. 9 (1968), 1220–1224.Google Scholar
[2]Arhangel’skii, A. V. & Tkachenko, M., Topological Groups and Related Structures (Atlantis Press, Amsterdam, 2008).CrossRefGoogle Scholar
[3]Engelking, R., ‘Cartesian products and dyadic spaces’, Fund. Math. 57 (1965), 287–304.CrossRefGoogle Scholar
[4]Engelking, R., General Topology (Heldermann, Berlin, 1989).Google Scholar
[5]Guran, I. I., ‘On topological groups close to being Lindelöf’, Soviet Math. Dokl. 23 (1981), 173–175.Google Scholar
[6]Hartman, S. & Mycielski, J., ‘On embeddings of topological groups into connected topological groups’, Colloq. Math. 5 (1958), 167–169.CrossRefGoogle Scholar
[7]Ivacovskij, L. N., ‘On a hypothesis of P. S. Alexandroff’, Dokl. Akad. Nauk SSSR 123 (1958), 785–786.Google Scholar
[8]Kodama, Y. & Nagami, K., General Topology (Iwanami Shoten, Tokyo, 1974).Google Scholar
[9]Malykhin, V. I. & Tironi, G., ‘Weakly Fréchet–Urysohn and Pytkeev spaces’, Topology Appl. 104 (2000), 181–190.CrossRefGoogle Scholar