Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T00:52:33.213Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Z. Jianzhong

Published online by Cambridge University Press:  17 April 2009

Yasuo Matsugu
Yasuo Matsugu
Affiliation:
Department of Mathematics Faculty of Science, Shinshu University, Matsumoto 390, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ϕ be a nonnegative, nondecreasing and nonconstant function defined on [0, ∞) such that Φ(t) = ϕ(et) is a convex function on (-∞, ∞). The Hardy-Orlicz space H (ϕ) is defined to be the class of all those functions f holomorphic in the open unit disc of the complex plane C satisfying The subclass H(ϕ)+ of H(ϕ) is defined to be the class of all those functions f ∈ H(ϕ) satisfying 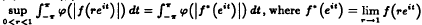for almost all points eit of the unit circle. In 1990, Z. Jianzhong conjectured that H(ϕ)+ = H(ψ)+ if and only if H(ϕ) = H(ψ). In the present paper we prove that it is true not only on the unit disc of C but also on the unit ball of Cn.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 45 , Issue 1 , February 1992 , pp. 163 - 170
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Deeb, W. and Marzuq, M., ‘H(φ) spaces’, Canad. Math. Bull. 29 (1986), 295–301.CrossRefGoogle Scholar
[2]Hahn, K. T., ‘Properties of holomorphic functions of bounded characteristic on star-shaped circular domains’, J. Reine Angew. Math. 254 (1972), 33–40.Google Scholar
[3]Hasumi, M. and Kataoka, S., ‘Remarks on Hardy-Orlicz classes’, Arch. Math. 51 (1988), 455–463.CrossRefGoogle Scholar
[4]Jianzhong, Z., ‘A note on Hardy-Orlicz spaces’, Canad. Math. Bull. 33 (1990), 29–33.CrossRefGoogle Scholar
[5]Khalil, R., ‘Inclusions of Hardy Orlicz spaces’, J. Math. and Math. Sci. 9 (1986), 429–434.CrossRefGoogle Scholar
[6]Priwalow, I.I., Randeigenschaften analytischer Funktionen (VEB Deutscher Verlag, Berlin, 1956).Google Scholar
[7]Rudin, W., Function theory in polydiscs (Benjamin, New York, 1969).Google Scholar
[8]Rudin, W., Function theory in the unit ball of Cn (Springer-Verlag, Berlin, Heidelberg, New York, 1980).CrossRefGoogle Scholar
[9]Rudin, W., New construction of functions holomorphic in the unit ball of Cn (NSF-CBMS Regional Conference No.63, 1985).CrossRefGoogle Scholar
[10]Stoll, M., ‘Mean growth and Fourier coefficients of some classes of holomorphic functions on bounded symmetric domains’, Ann. Polon. Math. 45 (1985), 161–183.CrossRefGoogle Scholar