Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-11T07:26:03.869Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A DUALITY THEOREM OF WAKAMATSU

Part of: Homological methods Modules, bimodules and ideals

Published online by Cambridge University Press:  01 October 2008

ZHAOYONG HUANG
ZHAOYONG HUANG*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China (email: huangzy@nju.edu.cn)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a left coherent ring, S a right coherent ring and RU a generalized tilting module, with S=End(RU) satisfying the condition that each finitely presented left R-module X with ExtRi(X,U)=0 for any i≥1 is U-torsionless. If M is a finitely presented left R-module such that ExtRi(M,U)=0 for any i≥0 with 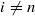(where n is a nonnegative integer), then 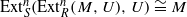and ExtSi(ExtRn(M,U),U)=0 for any i≥0 with 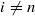. A duality is thus induced between the category of finitely presented holonomic left R-modules and the category of finitely presented holonomic right S-modules.

Keywords

generalized tilting modulesU-torsionless propertyFP-injective dimension

MSC classification

Secondary: 16E30: Homological functors on modules (Tor, Ext, etc.) 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 78 , Issue 2 , October 2008 , pp. 343 - 350
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Auslander, M. and Reiten, I., ‘Cohen-Macaulay and Gorenstein Artin algebras’, in: Representation Theory of Finite Groups and Finite-dimensional Algebras (Bielefeld, 1991), Progress in Mathematics, 95 (eds. G. O. Michler and C. M. Ringel) (Birkhauser, Basel, 1991), pp. 221–245.CrossRefGoogle Scholar
[2]Huang, Z. Y., ‘Selforthogonal modules with finite injective dimension III’, Algebr. Represent. Theory to appear.Google Scholar
[3]Huang, Z. Y. and Tang, G. H., ‘Self-orthogonal modules over coherent rings’, J. Pure Appl. Algebra 161 (2001), 167–176.CrossRefGoogle Scholar
[4]Miyashita, Y., ‘Tilting modules of finite projective dimension’, Math. Z. 193 (1986), 113–146.CrossRefGoogle Scholar
[5]Stenström, B., ‘Coherent rings and FP-injective modules’, J. London Math. Soc. 2 (1970), 323–329.CrossRefGoogle Scholar
[6]Wakamatsu, T., ‘Tilting modules and Auslander’s Gorenstein property’, J. Algebra 275 (2004), 3–39.CrossRefGoogle Scholar