Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-27T16:50:05.181Z Has data issue: false hasContentIssue false
  • English
  • Français

On a problem of Favard concerning algebraic integers

Published online by Cambridge University Press:  17 April 2009

C. W. Lloyd-Smith
C. W. Lloyd-Smith
Affiliation:
Australian Bureau of Statistics, Post Office Box 10, Belconnen, A.C.T., 2616, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let α be an algebraic integer of degree n > 1 with conjugates α = α1, α2, …, αn. Let D(α) denote the diameter of {α1, …, αn} and diam 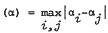. In 1929 Favard showed that diam 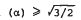and that, when n = 2 or 3, the minimal values of diam (α) are less than 2. The author shows that diam 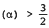and 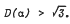He also finds all algebraic integers a with diam (α) ≤ 2 when n ≤ 5. Similar results are found for D(α) and, in particular, D(α) > 2 when n = 5.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 30 , Issue 1 , August 1984 , pp. 111 - 121
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Favard, J., “Sur les nombres algébriques”, C.R. Acad. Sc. Paris, 186 (1928), 1181–1182.Google Scholar
[2]Favard, J., “Sur les formes décomposables et les nombres algébriques”. Bull. Soc. Math. France 57 (1929), 50–71.Google Scholar
[3]Favard, J., “Sur les nombres algébriques”, Mathematica 4 (1930), 109–113.Google Scholar
[4]Kronecker, L., “Zwei Sätze über Gleichungen mit ganzzahligen Coefficienten”, J. reine angew. Math. 53 (1857), 173–175.Google Scholar
[5]Lloyd-Smith, C. W., “Problems on the distribution of conjugates of algebraic numbers”, Ph.D. Thesis, University of Adelaide, 1980.Google Scholar
[6]Robinson, R.M., “Conjugate algebraic integers on a circle”. Math. Z. 110 (1969), 41–51.Google Scholar
[7]Yaglom, I. M. and Bolyanskĭi, V. G., Convex Figures (translated by Kelly, Paul J. and Walton, Lewis F., Holt, Rinehart and Winston, New York, 1961).Google Scholar