Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T23:02:26.216Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A PROBLEM OF P. HALL FOR ENGEL WORDS II

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  13 May 2014

FRANCESCO G. RUSSO
FRANCESCO G. RUSSO*
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, 21945-970 Rio de Janeiro, Brasil Department of Mathematics and Applied Mathematics, University of Cape Town, Rondebosch 7701, Cape Town, South Africa email francescog.russo@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The present paper is related to some recent studies in Abdollahi and Russo [‘On a problem of P. Hall for Engel words’, Arch. Math. (Basel) 97 (2011), 407–412] and Fernández-Alcober et al. [‘A note on conciseness of Engel words’, Comm. Algebra 40 (2012), 2570–2576] on the position of the $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$-Engel marginal subgroup 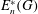$E^*_n(G)$ of a group 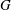$G$, when 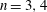$n=3,4$. Describing the size of 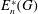$E^*_n(G)$ for 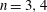$n=3,4$, we show some generalisations of classical results on the partial margins of 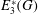$E^*_3(G)$ and $E^*_4(G)$.

Keywords

3-Engel groups4-Engel groupsmarginal subgroupscommutators

MSC classification

Secondary: 20E10: Quasivarieties and varieties of groups 20F45: Engel conditions 20F14: Derived series, central series, and generalizations 20D45: Automorphisms
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 237 - 246
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abdollahi, A., ‘Left 3-Engel elements in groups’, J. Pure Appl. Algebra 188 (2004), 1–6.CrossRefGoogle Scholar
Abdollahi, A., ‘Engel elements in groups’, in: Groups St Andrews 2009 in Bath, LMS Lecture Notes 387 (Cambridge University Press, Cambridge, 2011), 94–117.Google Scholar
Abdollahi, A. and Khosravi, H., ‘On the right and left 4-Engel elements’, Comm. Algebra 38 (2010), 933–943.Google Scholar
Abdollahi, A. and Khosravi, H., ‘Right 4-Engel elements of a group’, J. Algebra Appl. 9 (2010), 763–769.CrossRefGoogle Scholar
Abdollahi, A. and Russo, F. G., ‘On a problem of P. Hall for Engel words’, Arch. Math. (Basel) 97 (2011), 407–412.CrossRefGoogle Scholar
Fernández-Alcober, G. A., Morigi, M. and Traustason, G., ‘A note on conciseness of Engel words’, Comm. Algebra 40 (2012), 2570–2576.Google Scholar
Fernández-Alcober, G. A. and Shumyatsky, P., ‘On groups in which commutators are covered by finitely many cyclic subgroups’, J. Algebra 319 (2008), 4844–4851.Google Scholar
Gupta, N. D. and Newman, M. F., ‘Third Engel groups’, Bull. Aust. Math. Soc. 40 (1989), 215–230.CrossRefGoogle Scholar
Hall, P., ‘Verbal and marginal subgroups’, J. reine angew. Math. 182 (1940), 156–157.CrossRefGoogle Scholar
Havas, G. and Vaughan-Lee, M. R., ‘4-Engel groups are locally nilpotent’, Int. J. Algebra Comput. 15 (2005), 649–682.CrossRefGoogle Scholar
Heineken, H., ‘Engelsche Elemente der Länge drei’, Illinois J. Math. 5 (1961), 681–707.CrossRefGoogle Scholar
Kappe, L.-C., ‘Engel margins in metabelian groups’, Comm. Algebra 11 (1983), 165–187.CrossRefGoogle Scholar
Kappe, W. P., ‘Some subgroups defined by identities’, Illinois J. Math. 47 (2003), 317–326.Google Scholar
Kappe, L.-C. and Kappe, W. P., ‘On three-Engel groups’, Bull. Aust. Math. Soc. 7 (1972), 391–405.CrossRefGoogle Scholar
Newell, M., ‘On right Engel elements of length three’, Proc. Roy. Irish Acad. Sect. A 96 (1996), 17–24.Google Scholar
Nickel, W., ‘Some groups with right Engel elements’, in: Groups St. Andrews 1997 in Bath, LMS Lecture Notes 261 (Cambridge University Press, Cambridge, 1999), 571–578.CrossRefGoogle Scholar
Segal, D., ‘Words: notes on verbal width in groups’, LMS Lecture Notes 361 (Cambridge University Press, Cambridge, 2009).Google Scholar
Stroud, P., ‘On a property of verbal and marginal subgroups’, Proc. Camb. Philos. Soc. 61 (1965), 41–48.CrossRefGoogle Scholar
Teague, T. K., ‘On the Engel margin’, Pacific J. Math. 50 (1974), 205–214.CrossRefGoogle Scholar
The GAP Group, GAP—Groups, Algorithms and Programming (version 4.4, available at http://ww.gap-system.org, 2005).Google Scholar
Traustason, G., ‘On 4-Engel groups’, J. Algebra 178 (1995), 414–429.CrossRefGoogle Scholar
Traustason, G., ‘Locally nilpotent 4-Engel groups are Fitting groups’, J. Algebra 279 (2003), 7–27.CrossRefGoogle Scholar