Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T15:59:43.523Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ANALOGUES OF HUPPERT’S CONJECTURE

Part of: Representation theory of groups

Published online by Cambridge University Press:  18 January 2021

YONG YANG Open the ORCID record for YONG YANG [Opens in a new window]
YONG YANG*
Affiliation:
Key Laboratory of Group and Graph Theories and Applications, Chongqing University of Arts and Sciences, Chongqing, China and Department of Mathematics, Texas State University, 601 University Drive, San Marcos, TX 78666, USA
*
e-mail: yang@txstate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and 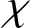$\chi $ be a character of G. The codegree of $\chi $ is 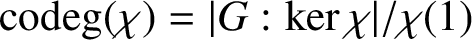${{\operatorname{codeg}}} (\chi ) ={|G: \ker \chi |}/{\chi (1)}$ . We write 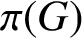$\pi (G)$ for the set of prime divisors of 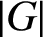$|G|$ 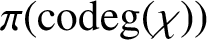, $\pi ({{\operatorname{codeg}}} (\chi ))$ for the set of prime divisors of 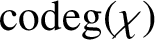${{\operatorname{codeg}}} (\chi )$ and 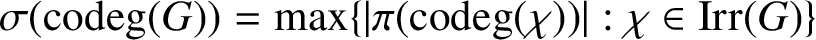$\sigma ({{\operatorname{codeg}}} (G))= \max \{|\pi ({{\operatorname{codeg}}} (\chi ))| : \chi \in {\textrm {Irr}}(G)\}$ . We show that 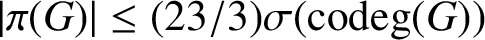$|\pi (G)| \leq ({23}/{3}) \sigma ({{\operatorname{codeg}}} (G))$ . This improves the main result of Yang and Qian [‘The analog of Huppert’s conjecture on character codegrees’, J. Algebra478 (2017), 215–219].

Keywords

charactercodegreefinite group

MSC classification

Primary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 272 - 277
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by the NSF of China (No. 11671063) and a grant from the Simons Foundation (No. 499532).

References

Bianchi, M., Chillag, D., Lewis, M. and Pacifici, E., ‘Character degree graphs that are complete graphs’, Proc. Amer. Math. Soc. 135 (2007), 671–676.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Dover, New York, 1994).Google Scholar
Isaacs, I. M., ‘Element orders and character codegrees’, Arch. Math. 97 (2011), 499–501.CrossRefGoogle Scholar
Keller, T. M., ‘A linear bound for $\rho (n)$ ’, J. Algebra 178 (1995), 643–652.CrossRefGoogle Scholar
Keller, T. M., ‘Solvable groups with at most four prime divisors in the element orders’, J. Algebra 175 (1995), 1–23.CrossRefGoogle Scholar
Liu, Y. and Yang, Y., ‘Nonsolvable groups with four character codegrees’, J. Algebra Appl., to appear.Google Scholar
Liu, Y. and Yang, Y., ‘Nonsolvable groups with five character codegrees’, Comm. Algebra, to appear.Google Scholar
Qian, G., ‘A note on element orders and character codegrees’, Arch. Math. 97 (2011), 99–103.CrossRefGoogle Scholar
Qian, G., Wang, Y. and Wei, H., ‘Co-degrees of irreducible characters in finite groups’, J. Algebra 312 (2007), 946–955.CrossRefGoogle Scholar
Rosser, J. B. and Schoenfeld, L., ‘Approximate formulas for some functions of prime numbers’, Illinois J. Math. 6 (1962), 64–94.CrossRefGoogle Scholar
Shi, W., ‘Characterization of finite simple groups and related topics’, Adv. in Math. (China) 20 (1991), 135–141.Google Scholar
Yang, Y. and Qian, G., ‘The analog of Huppert’s conjecture on character codegrees’, J. Algebra 478 (2017), 215–219.CrossRefGoogle Scholar
Zhang, J., ‘Arithmetical conditions on element orders and group structure’, Proc. Amer. Math. Soc. 123 (1995), 39–44.CrossRefGoogle Scholar