Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Parvatham, R.
and
Shanmugam, T.N.
1983.
On analytic functions with reference to an integral operator.
Bulletin of the Australian Mathematical Society,
Vol. 28,
Issue. 2,
p.
207.
Kumar, Vinod
and
Shukla, S.L.
1984.
On p–valent starlike functions with reference to the Bernardi integral operator.
Bulletin of the Australian Mathematical Society,
Vol. 30,
Issue. 1,
p.
37.
Noor, Khalida Inayat
1987.
On some univalent integral operators.
Journal of Mathematical Analysis and Applications,
Vol. 128,
Issue. 2,
p.
586.
Jian, Ming
1994.
ON THE CLASS Φ p * (a,ß,γ,ɛ,η;A) of p -VALENT FUNCTIONS WITH REFERENCE TO THE BERNARDI INTEGRAL OPERATOR.
Acta Mathematica Scientia,
Vol. 14,
Issue. 4,
p.
371.
Aouf, M.K.
and
Ling, Yi
2009.
Some convolution properties of a certain class of p-valent analytic functions.
Applied Mathematics Letters,
Vol. 22,
Issue. 3,
p.
361.
Ibrahim
2010.
On Certain Classes of Multivalent Analytic Functions.
Journal of Mathematics and Statistics,
Vol. 6,
Issue. 3,
p.
271.
Eljamal, E. A.
Darus, M.
and
Breaz, D.
2013.
Some Results of Univalent and Starlike Integral Operator.
Journal of Complex Analysis,
Vol. 2013,
Issue. ,
p.
1.
Bucur, Roberta
Andrei, Loriana
and
Breaz, Daniel
2015.
Geometric Properties of a New Integral Operator.
Abstract and Applied Analysis,
Vol. 2015,
Issue. ,
p.
1.
Bucur, Roberta
Andrei, Loriana
and
Breaz, Daniel
2016.
Properties of a new integral operator.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 24,
Issue. 2,
p.
127.
Jafari, Mostafa
Motamednezad, Ahmad
and
Adegani, Ebrahim Analouei
2022.
Coefficient estimates for a subclass of analytic functions by Srivastava-Attiya operator.
Studia Universitatis Babes-Bolyai Matematica,
Vol. 67,
Issue. 4,
p.
739.
Lashin, Abdel Moneim Y.
and
Aouf, Mohamed K.
2022.
Hadamard Product of Certain Multivalent Analytic Functions with Positive Real Parts.
Mathematics,
Vol. 10,
Issue. 9,
p.
1506.


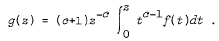
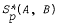 of
of 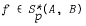 then
then