Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-13T21:54:13.407Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ASYMPTOTIC BASES WHICH HAVE DISTINCT SUBSET SUMS

Part of: Sequences and sets

Published online by Cambridge University Press:  12 April 2021

SÁNDOR Z. KISS Open the ORCID record for SÁNDOR Z. KISS [Opens in a new window]  and
VINH HUNG NGUYEN Open the ORCID record for VINH HUNG NGUYEN [Opens in a new window]
SÁNDOR Z. KISS*
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, H-1529 B.O. Box, Budapest, Hungary
VINH HUNG NGUYEN
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, H-1529 B.O. Box, Budapest, Hungary e-mail: nguyenvinhhung108@gmail.com
*
e-mail: kisspest@cs.elte.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

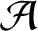Let k and l be positive integers satisfying $k \ge 2, l \ge 1$ . A set $\mathcal {A}$ of positive integers is an asymptotic basis of order k if every large enough positive integer can be represented as the sum of k terms from 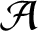$\mathcal {A}$ . About 35 years ago, P. Erdős asked: does there exist an asymptotic basis of order k where all the subset sums with at most l terms are pairwise distinct with the exception of a finite number of cases as long as $l \le k - 1$ ? We use probabilistic tools to prove the existence of an asymptotic basis of order 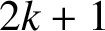$2k+1$ for which all the sums of at most k elements are pairwise distinct except for ‘small’ numbers.

Keywords

additive number theoryasymptotic basisprobabilistic methodSidon set

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11B75: Other combinatorial number theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 211 - 217
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Research, Development and Innovation Office NKFIH Grant Nos. K115288 and K129335. This paper was supported by a János Bolyai Research Scholarship of the Hungarian Academy of Sciences, by the ÚNKP-19-4 New National Excellence Program of the Ministry for Innovation and Technology and by the ÚNKP-20-5 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund.

References

Cilleruelo, J., ‘On Sidon sets and asymptotic bases’, Proc. Lond. Math. Soc. 111 (2015), 1206–1230.CrossRefGoogle Scholar
Deshouillers, J. M. and Plagne, A., ‘A Sidon basis’, Acta Math. Hungar. 123 (2009), 233–238.CrossRefGoogle Scholar
Erdős, P., ‘Some applications of probability methods to number theory’, in: Mathematical Statistics and Applications, Bad Tatzmannsdord, 1983, Vol. B (Springer, Dordrecht, 1985), 1–18.Google Scholar
Erdős, P., Sárközy, A. and Sós, V. T., ‘On additive properties of general sequences’, Discrete Math. 136 (1994), 75–99.CrossRefGoogle Scholar
Erdős, P., Sárközy, A. and Sós, V. T., ‘On sum sets of Sidon sets I’, J. Number Theory 47 (1994), 329–347.CrossRefGoogle Scholar
Erdős, P. and Spencer, J., Probabilistic Methods in Combinatorics (Akadémiai Kiadó, Budapest, 1974).Google Scholar
Erdős, P. and Tetali, P., ‘Representations of integers as the sum of $k$ terms’, Random Structures Algorithms 1 (1990), 245–261.CrossRefGoogle Scholar
Erdős, P. and Turán, P., ‘On a problem of Sidon in additive number theory, and some related problems’, J. Lond. Math. Soc. 16 (1941), 212–215.CrossRefGoogle Scholar
Halberstam, H. and Roth, K. F., Sequences (Springer, New York, 1983).CrossRefGoogle Scholar
Kiss, S. Z., ‘On Sidon sets which are asymptotic bases’, Acta Math. Hungar. 128 (2010), 46–58.CrossRefGoogle Scholar
Kiss, S. Z., ‘On generalized Sidon sets which are asymptotic bases’, Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 57 (2014), 149–160.Google Scholar
Kiss, S. Z., Rozgonyi, E. and Sándor, C., ‘On Sidon sets which are asymptotic bases of order 4’, Funct. Approx. Comment. Math. 51 (2014), 393–413.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., ‘Generalized asymptotic Sidon basis’, Discrete Math. 344 (2021), 112208.CrossRefGoogle Scholar