Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ballester-Bolinches, A.
Pedraza-Aguilera, M. C.
and
Pérez-Ramos, M. D.
1998.
Finite groups which are products of pairwise totally permutable subgroups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 41,
Issue. 3,
p.
567.
Ballester-Bolinches, A.
and
Pedraza-Aguilera, M. C.
1999.
On finite soluble products of 𝒩-connected groups.
Journal of Group Theory,
Vol. 2,
Issue. 3,
Beidleman, J.
and
Heineken, H.
1999.
Totally permutable torsion subgroups.
Journal of Group Theory,
Vol. 2,
Issue. 4,
Ballester-Bolinches, A.
and
Pedraza-Aguilera, M.C.
1999.
Mutually Permutable Products of Finite Groups, II.
Journal of Algebra,
Vol. 218,
Issue. 2,
p.
563.
Ballester-Bolinches, A.
Pérez-Ramos, M.D.
and
Pedraza-Aguilera, M.C.
1999.
Mutually Permutable Products of Finite Groups.
Journal of Algebra,
Vol. 213,
Issue. 1,
p.
369.
Beidleman, James
Hauck, Peter
and
Heineken, Hermann
2004.
Totally permutable products of certain classes of finite groups.
Journal of Algebra,
Vol. 276,
Issue. 2,
p.
826.
Ballester-Bolinches, A.
Cossey, John
and
Pedraza-Aguilera, M.C.
2005.
On mutually permutable products of finite groups.
Journal of Algebra,
Vol. 294,
Issue. 1,
p.
127.
Arroyo-Jordá, M.
Arroyo-Jordá, P.
and
Pérez-Ramos, M. D.
2011.
On conditional permutability and saturated formations.
Proceedings of the Edinburgh Mathematical Society,
Vol. 54,
Issue. 2,
p.
309.
Madanha, S.Y.
2012.
On a generalisation of totally permutable products of finite groups.
Journal of Algebra,
Vol. 358,
Issue. ,
p.
1.
Naraghi, Hassan
2012.
Some properties of the supersoluble formation and the supersoluble residual of a group.
Mathematical Sciences,
Vol. 6,
Issue. 1,
p.
39.
Ballester-Bolinches, A.
Beidleman, J. C.
Heineken, H.
and
Pedraza-Aguilera, M. C.
2013.
Prefactorized subgroups in pairwise mutually permutable products.
Annali di Matematica Pura ed Applicata,
Vol. 192,
Issue. 6,
p.
1043.
Arroyo-Jordá, M.
Arroyo-Jordá, P.
Martínez-Pastor, A.
and
Pérez-Ramos, M. D.
2014.
On conditional permutability and factorized groups.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 193,
Issue. 4,
p.
1123.
Guo, Wenbin
and
Kondrat’ev, A. S.
2015.
Finite Minimal Non-supersolvable Groups Decomposable into the Product of Two Normal Supersolvable Subgroups.
Communications in Mathematics and Statistics,
Vol. 3,
Issue. 2,
p.
285.
Li, X.
and
Wu, X.
2024.
The formation residual of factorized finite groups.
Acta Mathematica Hungarica,
Vol. 174,
Issue. 1,
p.
202.


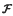 -residual, where
-residual, where 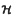 -projectors and
-projectors and 