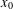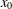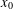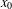Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pawlak, Ryszard J.
and
Korczak-Kubiak, Ewa
2018.
Dynamical Systems in Theoretical Perspective.
Vol. 248,
Issue. ,
p.
271.
Loranty, Anna
Pawlak, Ryszard J.
and
Terepeta, Małgorzata
2019.
On almost continuous functions and peculiar points.
European Journal of Mathematics,
Vol. 5,
Issue. 1,
p.
106.