Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T12:54:44.390Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION

Part of: Diophantine approximation, transcendental number theory Other groups of matrices

Published online by Cambridge University Press:  25 January 2021

LUCA MARCHESE Open the ORCID record for LUCA MARCHESE [Opens in a new window]
LUCA MARCHESE*
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta San Donato 5, 40126Bologna, Italy
*
e-mail: luca.marchese4@unibo.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the continued fraction expansion of real numbers under the action of a nonuniform lattice in 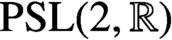$\text {PSL}(2,{\mathbb R})$ and prove metric relations between the convergents and a natural geometric notion of good approximations.

Keywords

continued fractionsFuchsian groups

MSC classification

Primary: 11J70: Continued fractions and generalizations
Secondary: 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 45 - 58
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artigiani, M., Marchese, L. and Ulcigrai, C., ‘The Lagrange spectrum of a Veech surface has a Hall ray’, Groups Geom. Dyn. 10 (2016), 1287–1337.CrossRefGoogle Scholar
Artigiani, M., Marchese, L. and Ulcigrai, C., ‘Persistent Hall rays for Lagrange spectra at cusps of Riemann surfaces’, Ergod. Th. & Dynam. Sys. 40(8) (2020), 2017–2072.CrossRefGoogle Scholar
Bowen, R. and Series, C., ‘Markov maps associated with fuchsian groups’, Publ. Math. Inst. Hautes Études Sci. 50 (1979), 153–170.CrossRefGoogle Scholar
Katok, S., Fuchsian Groups, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1992).Google Scholar
Lehner, J., ‘Diophantine approximation on Hecke groups’, Glasg. Math. J. 27 (1985), 117–127.CrossRefGoogle Scholar
Marchese, L., ‘Transfer operators and dimension of bad sets for non-uniform Fuchsian lattices’, Preprint, 2018, arXiv:1812.11921.Google Scholar
Nakada, H., ‘On the Lenstra constant associated to the Rosen continued fractions’, J. Eur. Math. Soc. 12 (2010), 55–70.CrossRefGoogle Scholar
Patterson, S. J., ‘Diophantine approximation in Fuchsian groups’, Philos. Trans. Roy. Soc. Lond. Ser. A 282(1309) (1976), 527–563.Google Scholar
Rosen, D., ‘A class of continued fractions associated to certain properly discontinuous groups’, Duke Math. J. 21 (1954), 549–562.CrossRefGoogle Scholar
Rosen, D. and Schmidt, T., ‘Hecke groups and continued fractions’, Bull. Aust. Math. Soc. 46 (1992), 459–474.CrossRefGoogle Scholar
Schmidt, T. and Sheingorn, M., ‘Riemann surfaces have Hall rays at each cusp’, Illinois J. Math. 41(3) (1997), 378–397.CrossRefGoogle Scholar
Tukia, P., ‘On discrete groups of the unit disk and their isomorphisms’, Ann. Acad. Sci. Fenn. Ser. A I 504 (1972), 1–45.Google Scholar