Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-27T01:31:19.998Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GUILLERA’S 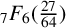${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR 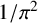${1}/{\pi ^2}$

Part of: Acceleration of convergence Computational aspects

Published online by Cambridge University Press:  09 February 2023

JOHN M. CAMPBELL Open the ORCID record for JOHN M. CAMPBELL [Opens in a new window]
JOHN M. CAMPBELL*
Affiliation:
Department of Mathematics, Toronto Metropolitan University, Toronto, Ontario, Canada
*
e-mail: jmaxwellcampbell@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In 2011, Guillera [‘A new Ramanujan-like series for 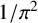$1/\pi ^2$’, Ramanujan J. 26 (2011), 369–374] introduced a remarkable rational 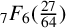${}_{7}F_{6}( \frac {27}{64} )$-series for 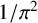${1}/{\pi ^2}$ using the Wilf–Zeilberger (WZ) method, and Chu and Zhang later proved this evaluation using an acceleration method based on Dougall’s 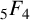${}_{5}F_{4}$-sum. Another proof of Guillera’s 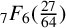${}_{7}F_{6}( \frac {27}{64} )$-series was given by Guillera in 2018, and this subsequent proof used a recursive argument involving Dougall’s sum together with the WZ method. Subsequently, Chen and Chu introduced a q-analogue of Guillera’s ${}_{7}F_{6}( \frac {27}{64} )$-series. The many past research articles concerning Guillera’s ${}_{7}F_{6}( \frac {27}{64} )$-series for 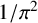${1}/{\pi ^2}$ naturally lead to questions about similar results for other mathematical constants. We apply a WZ-based acceleration method to prove new rational 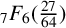${}_{7}F_{6}( \frac {27}{64} )$- and 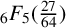${}_{6}F_{5}( \frac {27}{64} )$-series for 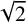$\sqrt {2}$.

Keywords

series accelerationWZ methodinfinite seriesclosed form

MSC classification

Primary: 33F10: Symbolic computation (Gosper and Zeilberger algorithms, etc.)
Secondary: 65B10: Summation of series
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 464 - 471
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, W. N., Generalized Hypergeometric Series (Cambridge University Press, Cambridge, 1935).Google Scholar
Beukers, F. and Forsgøard, J., ‘ $\varGamma$ -evaluations of hypergeometric series’, Ramanujan J. 58 (2022), 677–699.10.1007/s11139-022-00566-4CrossRefGoogle Scholar
Campbell, J. M., ‘WZ proofs of identities from Chu and Kılıç, with applications’, Appl. Math. E-Notes 22 (2022), 354–361.Google Scholar
Chen, X. and Chu, W., ‘ $q$ -analogues of Guillera’s two series for ${\pi}^{\pm 2}$ with convergence rate $\frac{27}{64}$ ’, Int. J. Number Theory 17 (2021), 71–90.10.1142/S1793042121500056CrossRefGoogle Scholar
Chu, W., ‘Terminating ${}_2{F}_1(4)$ -series perturbed by two integer parameters’, Proc. Amer. Math. Soc. 145 (2017), 1031–1040.10.1090/proc/13293CrossRefGoogle Scholar
Chu, W., ‘Infinite series formulae related to Gauss and Bailey -sums’, Acta Math. Sci. Ser. B (Engl. Ed.) 40 (2020), 293–315.Google Scholar
Chu, W., ‘Seven hundreds of exotic ${}_3{F}_2$ -series evaluated in $\pi$ , $\sqrt{2}$ and $\log (1+\sqrt{2})$ ’, Contemp. Math. 2 (2021), 327–398.10.37256/cm.2420211066CrossRefGoogle Scholar
Chu, W. and Kılıç, E., ‘Binomial sums involving Catalan numbers’, Rocky Mountain J. Math. 51 (2021), 1221–1225.10.1216/rmj.2021.51.1221CrossRefGoogle Scholar
Chu, W. and Zhang, W., ‘Accelerating Dougall’s ${}_5{F}_4$ -sum and infinite series involving $\pi$ ’, Math. Comput. 83 (2014), 475–512.10.1090/S0025-5718-2013-02701-9CrossRefGoogle Scholar
Ebisu, A., ‘On a strange evaluation of the hypergeometric series by Gosper’, Ramanujan J. 32 (2013), 101–108.10.1007/s11139-013-9483-1CrossRefGoogle Scholar
Ebisu, A., ‘Special values of the hypergeometric series’, Mem. Amer. Math. Soc. 248 (2017), 1–96.Google Scholar
Ekhad, S. B., ‘Forty “strange” computer-discovered [and computer-proved (of course!)] hypergeometric series evaluations’, Personal Journal of Shalosh B. Ekhad and Doron Zeilberger, 2004. https://sites.math.rutgers.edu/zeilberg/mamarim/mamarimhtml/strange.html.Google Scholar
Guillera, J., ‘Some binomial series obtained by the WZ-method’, Adv. Appl. Math. 29 (2002), 599–603.10.1016/S0196-8858(02)00034-9CrossRefGoogle Scholar
Guillera, J., ‘Generators of some Ramanujan formulas’, Ramanujan J. 11 (2006), 41–48.10.1007/s11139-006-5306-yCrossRefGoogle Scholar
Guillera, J., ‘A new method to obtain series for $1/\pi$ and $1/ {\pi}^2$ ’, Exp. Math. 15 (2006), 83–89.10.1080/10586458.2006.10128943CrossRefGoogle Scholar
Guillera, J., ‘Hypergeometric identities for 10 extended Ramanujan-type series’, Ramanujan J. 15 (2008), 219–234.10.1007/s11139-007-9074-0CrossRefGoogle Scholar
Guillera, J., ‘On WZ-pairs which prove Ramanujan series’, Ramanujan J. 22 (2010), 249–259.10.1007/s11139-010-9238-1CrossRefGoogle Scholar
Guillera, J., ‘A new Ramanujan-like series for $1/ {\pi}^2$ ’, Ramanujan J. 26 (2011), 369–374.10.1007/s11139-010-9259-9CrossRefGoogle Scholar
Guillera, J., ‘Dougall’s ${}_5{F}_4$ sum and the WZ algorithm’, Ramanujan J. 46 (2018), 667–675.10.1007/s11139-018-9998-6CrossRefGoogle Scholar
Mao, G.-S. and Tauraso, R., ‘Three pairs of congruences concerning sums of central binomial coefficients’, Int. J. Number Theory 17 (2021), 2301–2314.10.1142/S1793042121500895CrossRefGoogle Scholar
Marichev, O., Sondow, J. and Weisstein, E. W., ‘Catalan’s Constant’, from MathWorld–A Wolfram Web Resource, 2022. https://mathworld.wolfram.com/CatalansConstant.html.Google Scholar
Oerlemans, A. H. M., The Cupproduct’s Applications to Ebisu’s Method, Master Thesis, Universiteit Utrecht, 2019.Google Scholar
Petkovšek, M., Wilf, H. S. and Zeilberger, D., $A=B$ (A. K. Peters, Ltd., Wellesley, MA, 1996).Google Scholar
Rainville, E. D., Special Functions (The Macmillan Company, New York, 1960).Google Scholar
Weisstein, E. W., ‘Apéry’s Constant’, from MathWorld–A Wolfram Web Resource, 2022. https://mathworld.wolfram.com/AperysConstant.html.Google Scholar
Weisstein, E. W., ‘Pi Squared’, from MathWorld–A Wolfram Web Resource, 2022. https://mathworld.wolfram.com/PiSquared.html.Google Scholar
Weisstein, E. W., ‘Pythagoras’s constant’, from MathWorld–A Wolfram Web Resource, 2022. https://mathworld.wolfram.com/PythagorassConstant.html.Google Scholar