Article contents
ON INTEGER SETS WITH THE SAME REPRESENTATION FUNCTIONS
Published online by Cambridge University Press: 03 March 2022
Abstract
Let 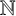 $\mathbb {N}$ be the set of all nonnegative integers. For
$\mathbb {N}$ be the set of all nonnegative integers. For 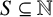 $S\subseteq \mathbb {N}$ and
$S\subseteq \mathbb {N}$ and 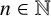 $n\in \mathbb {N}$, let
$n\in \mathbb {N}$, let 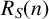 $R_S(n)$ denote the number of solutions of the equation
$R_S(n)$ denote the number of solutions of the equation 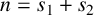 $n=s_1+s_2$,
$n=s_1+s_2$, 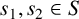 $s_1,s_2\in S$ and
$s_1,s_2\in S$ and 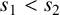 $s_1<s_2$. Let A be the set of all nonnegative integers which contain an even number of digits
$s_1<s_2$. Let A be the set of all nonnegative integers which contain an even number of digits 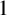 $1$ in their binary representations and
$1$ in their binary representations and 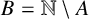 $B=\mathbb {N}\setminus A$. Put
$B=\mathbb {N}\setminus A$. Put 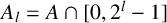 $A_l=A\cap [0,2^l-1]$ and
$A_l=A\cap [0,2^l-1]$ and 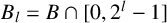 $B_l=B\cap [0,2^l-1]$. We prove that if
$B_l=B\cap [0,2^l-1]$. We prove that if 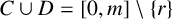 $C \cup D=[0, m]\setminus \{r\}$ with
$C \cup D=[0, m]\setminus \{r\}$ with 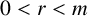 $0<r<m$,
$0<r<m$, 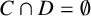 $C \cap D=\emptyset $ and
$C \cap D=\emptyset $ and 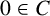 $0 \in C$, then
$0 \in C$, then 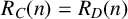 $R_{C}(n)=R_{D}(n)$ for any nonnegative integer n if and only if there exists an integer
$R_{C}(n)=R_{D}(n)$ for any nonnegative integer n if and only if there exists an integer 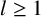 $l \geq 1$ such that
$l \geq 1$ such that 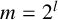 $m=2^{l}$,
$m=2^{l}$, 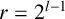 $r=2^{l-1}$,
$r=2^{l-1}$, 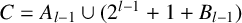 $C=A_{l-1} \cup (2^{l-1}+1+B_{l-1})$ and
$C=A_{l-1} \cup (2^{l-1}+1+B_{l-1})$ and 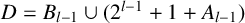 $D=B_{l-1} \cup (2^{l-1}+1+A_{l-1})$. Kiss and Sándor [‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161] proved an analogous result when
$D=B_{l-1} \cup (2^{l-1}+1+A_{l-1})$. Kiss and Sándor [‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161] proved an analogous result when 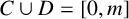 $C\cup D=[0,m]$,
$C\cup D=[0,m]$, 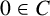 $0\in C$ and
$0\in C$ and 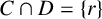 $C\cap D=\{r\}$.
$C\cap D=\{r\}$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 224 - 235
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The second author was supported by the OTKA Grant No. K129335
References
- 3
- Cited by


