Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T09:20:39.145Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ISOMETRIC REPRESENTATION SUBSETS OF BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  11 December 2015

YU ZHOU ,
ZIHOU ZHANG  and
CHUNYAN LIU
YU ZHOU*
Affiliation:
School of Fundamental Studies, Shanghai University of Engineering Science, Shanghai, 201620, PR China email roczhou_fly@126.com
ZIHOU ZHANG
Affiliation:
School of Fundamental Studies, Shanghai University of Engineering Science, Shanghai, 201620, PR China email zhz@sues.edu.cn
CHUNYAN LIU
Affiliation:
School of Fundamental Studies, Shanghai University of Engineering Science, Shanghai, 201620, PR China email cyl@sues.edu.cn
*
✉roczhou_fly@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

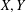Let $X,Y$ be two Banach spaces and 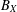$B_{X}$ the closed unit ball of 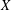$X$. We prove that if there is an isometry 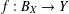$f:B_{X}\rightarrow Y$ with 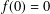$f(0)=0$, then there exists an isometry 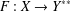$F:X\rightarrow Y^{\ast \ast }$. If, in addition, 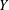$Y$ is weakly nearly strictly convex, then there is an isometry 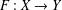$F:X\rightarrow Y$. Making use of these results, we show that if 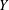$Y$ is weakly nearly strictly convex and there is an isometry 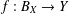$f:B_{X}\rightarrow Y$ with 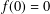$f(0)=0$, then there exists a linear isometry 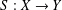$S:X\rightarrow Y$.

Keywords

representation subset of isometryisometrylinear isometryBanach space

MSC classification

Primary: 46B04: Isometric theory of Banach spaces
Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 3 , June 2016 , pp. 486 - 496
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis I, American Mathematical Society Colloquium Publications, 48 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Cabrera, J. and Sadarangani, B., ‘Weak near convexity and smoothness of Banach spaces’, Arch. Math. 78 (2002), 126–134.Google Scholar
Cheng, L., Dong, Y. and Zhang, W., ‘On stability of nonlinear non-surjective 𝜖-isometries of Banach spaces’, J. Funct. Anal. 264 (2013), 713–734.CrossRefGoogle Scholar
Cheng, L. and Zhou, Y., ‘On perturbed metric-preserved mappings and their stability characterizations’, J. Funct. Anal. 266 (2014), 4995–5015.CrossRefGoogle Scholar
Dutrieux, Y. and Lancien, G., ‘Isometric embeddings of compact spaces into Banach spaces’, J. Funct. Anal. 255 (2008), 494–501.CrossRefGoogle Scholar
Figiel, T., ‘On non linear isometric embeddings of normed linear spaces’, Bull. Acad. Pol. Sci. Math. Astron. Phys. 16 (1968), 185–188.Google Scholar
Godefroy, G., ‘Linearization of isometric embeddings between Banach spaces: an elementary approach’, Oper. Matrices 6(2) (2012), 339–345.CrossRefGoogle Scholar
Godefroy, G. and Kalton, N. J., ‘Lipschitz-free Banach spaces’, Studia Math. 159 (2003), 121–141.Google Scholar
Mazur, S. and Ulam, S., ‘Sur les transformations isométriques d’espaces vectoriels normés’, C. R. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Phelps, R., Convex Functions, Monotone Operators and Differentiability, Lecture Notes in Mathematics, 1364 (Springer, Berlin, 1989).Google Scholar
Vestfrid, I. A., ‘Stability of almost surjective 𝜀-isometries of Banach spaces’, J. Funct. Anal. 269 (2015), 2165–2170.Google Scholar