Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-26T11:16:10.006Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MINIMAL ADDITIVE COMPLEMENTS

Part of: Sequences and sets

Published online by Cambridge University Press:  11 February 2025

GUO WANYAN Open the ORCID record for GUO WANYAN [Opens in a new window]  and
MIN TANG Open the ORCID record for MIN TANG [Opens in a new window]
GUO WANYAN
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241002, PR China e-mail: gwy202411@163.com
MIN TANG*
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241002, PR China
*
e-mail: tmzzz2000@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let C and W be two integer sets. If 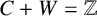$C+W=\mathbb {Z}$, then we say that C is an additive complement to W. If no proper subset of C is an additive complement to W, then we say that C is a minimal additive complement to W. We study the existence of a minimal additive complement to 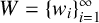$W=\{w_i\}_{i=1}^{\infty}$ when W is not eventually periodic and 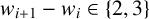$w_{i+1}-w_{i}\in \{2,3\}$ for all i.

Keywords

additive complementsminimal additive complementseventually periodic set

MSC classification

Primary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the National Natural Science Foundation of China (Grant No. 12371003).

References

Alon, N., Kravitz, N. and Larson, M., ‘Inverse problems for minimal complements and maximal supplements’, J. Number Theory 223 (2021), 307–324.CrossRefGoogle Scholar
Biswas, A. and Saha, J. P., ‘On minimal complements in groups’, Ramanujan J. 55 (2021), 823–847.CrossRefGoogle Scholar
Burcroff, A. and Luntzlara, N., ‘Sets arising as minimal additive complements in the integers’, J. Number Theory 247 (2023), 15–34.CrossRefGoogle Scholar
Chen, Y. G. and Yang, Q. H., ‘On a problem of Nathanson related to minimal additive complements’, SIAM J. Discrete Math. 26 (2012), 1532–1536.CrossRefGoogle Scholar
Cohen, G., Honkala, I., Litsyn, S. and Lobstein, A., Covering Codes, North-Holland Mathematical Library, 54 (Elsevier, Amsterdam, 1997).Google Scholar
Kiss, S. Z., Sándor, C. and Yang, Q. H., ‘On minimal additive complements of integers’, J. Combin. Theory Ser. A 162 (2019), 344–353.CrossRefGoogle Scholar
Kwon, A., ‘A note on minimal additive complements of integers’, Discrete Math. 342 (2019), 1912–1918.CrossRefGoogle Scholar
Nathanson, M. B., ‘Problems in additive number theory, IV: nets in groups and shortest length $g$ -adic representations’, Int. J. Number Theory 7 (2011), 1999–2017.CrossRefGoogle Scholar
Zhou, F., ‘On eventually periodic sets as minimal additive complements’, Electron. J. Combin. 30 (2023), Article no. 4.34.CrossRefGoogle Scholar