Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-30T19:37:14.585Z Has data issue: false hasContentIssue false
  • English
  • Français

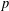ON $p$-PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  28 March 2018

YONG YANG Open the ORCID record for YONG YANG [Opens in a new window]  and
GUOHUA QIAN
YONG YANG*
Affiliation:
Department of Mathematics, Texas State University, 601 University Drive, San Marcos, TX 78666, USA Key Laboratory of Group and Graph Theories and Applications, Chongqing University of Arts and Sciences, Chongqing, PR China email yang@txstate.edu
GUOHUA QIAN
Affiliation:
Department of Mathematics, Changshu Institute of Technology, Changshu, JiangSu 215500, PR China email ghqian2000@163.com
*
✉yang@txstate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 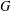$G$ be a finite group. Let 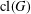$\operatorname{cl}(G)$ be the set of conjugacy classes of 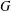$G$ and let 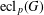$\operatorname{ecl}_{p}(G)$ be the largest integer such that 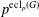$p^{\operatorname{ecl}_{p}(G)}$ divides 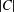$|C|$ for some 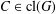$C\in \operatorname{cl}(G)$. We prove the following results. If 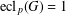$\operatorname{ecl}_{p}(G)=1$, then 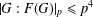$|G:F(G)|_{p}\leq p^{4}$ if 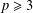$p\geq 3$. Moreover, if 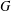$G$ is solvable, then 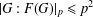$|G:F(G)|_{p}\leq p^{2}$.

Keywords

conjugacy class sizes

MSC classification

Primary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 406 - 411
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The project was supported by NSFC (Nos. 11671063 and 11471054), the Natural Science Foundation Project of CSTC (cstc2016jcyjA0065) and the NSF of Jiangsu Province (No. BK20161265). The first author was also supported by a grant from the Simons Foundation (No. 499532).

References

Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups (Oxford University Press, New York, 1985).Google Scholar
Lewis, M., Navarro, G., Tiep, P. H. and Tong-Viet, H. P., ‘ p-parts of character degrees’, J. Lond. Math. Soc. (2) 92 (2015), 483–497.CrossRefGoogle Scholar
Lewis, M., Navarro, G. and Wolf, T. R., ‘ p-parts of character degrees and the index of the Fitting subgroup’, J. Algebra 411 (2014), 182–190.Google Scholar
Liu, X., Wang, Y. and Wei, H., ‘Notes on the length of conjugacy classes of finite groups’, J. Pure Appl. Algebra 196 (2005), 111–117.Google Scholar
Michler, G., ‘A finite simple group of Lie type has p-blocks with different defects, p≠2’, J. Algebra 104(2) (1986), 220–230.Google Scholar
Qian, G. and Wang, Y., ‘A note on the conjugacy class sizes of finite groups’, Acta Math. Sci. Chin. Ser. 52(1) (2009), 125–130.Google Scholar