Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T16:38:20.315Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SCHRÖDINGER EQUATIONS WITH INDEFINITE NONLINEARITIES

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  10 March 2009

JING LONG  and
JIANFU YANG
JING LONG
Affiliation:
Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, P.O. Box 71010, Wuhan 430071 Graduate School, Chinese Academy of Sciences, Beijing 100049, People’s Republic of China (email: alongjing@yahoo.com.cn)
JIANFU YANG*
Affiliation:
Department of Mathematics, Jiangxi Normal University, Nanchang, Jiangxi, 330022, People’s Republic of China (email: jfyang_2000@yahoo.com)
*
✉For correspondence; e-mail: jfyang_2000@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the problem of finding standing waves – solutions to nonlinear Schrödinger equations with vanishing potential and sign-changing nonlinearities. This involves searching for solutions of the problem (1)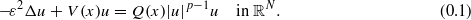We show that the problem has a solution, and the maximum point of the solution is concentrated on a minimum point of some function as ε→0.

Keywords

Schrödinger equationweighted Sobolev spaceconcentration

MSC classification

Secondary: 35J20: Variational methods for second-order elliptic equations 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 1 , February 2009 , pp. 115 - 128
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

This work was supported by National Natural Sciences Foundations of China, No: 10571175 and 10631030.

References

[1] Alama, S. and Del Pino, M., ‘Solution of elliptic equations with indefinite nonlinearities via Morse theory and linking’, Ann. Inst. H. Poincaré, Anal. Non Linéaire 13 (1996), 95–115.Google Scholar
[2] Ambrosetti, A., Felli, V. and Malchiodi, A., ‘Ground states of nonlinear Schrödinger equations with potentials vanishing at infinity’, J. Eur. Math. Soc. 7 (2005), 117–144.Google Scholar
[3] Brezis, H. and Lieb, E., ‘A relation between pointwise convergence of functions and convergence of functions’, Proc. Amer. Math. Soc. 88 (1983), 486–490.Google Scholar
[4] Costa, D. G. and Tehrani, H., ‘Existence of positive solutions for a class of indefinite elliptic problems in ℝN’, Calc. Var. Partial Differential Equations 13 (2001), 159–189.Google Scholar
[5] Gidas, B., Ni, W.-M. and Nirenberg, L., ‘Symmetry of positive solutions of nonlinear elliptic equations in ℝN’, Adv. Math. Suppl. Stud. 7A (1981), 369–402. (Math. Anal. Appl. Part A).Google Scholar
[6] Ni, W.-M. and Takagi, I., ‘On the shape of least-energy solutions to a semilinear Neumann problem’, Comm. Pure Appl. Math. XLIV (1991), 819–851.Google Scholar
[7] Rabinowitz, P. H., ‘On a class of nonlinear Schrödinger equations’, Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
[8] Rabinowitz, P. H., Minmax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics, 65 (American Mathematical Society, Providence, RI, 1986).Google Scholar
[9] Wang, X.-F., ‘On concentration of positive bound states of nonlinear Schrödinger equations’, Comm. Math. Phys. 153 (1993), 229–244.CrossRefGoogle Scholar
[10] Wang, X.-F. and Zeng, B., ‘On concentration of positive bound states of nonlinear Schrödinger equations with competing potential functions’, SIAM J. Math. Anal. 28 (1997), 633–655.CrossRefGoogle Scholar