Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:50:37.507Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOLUTIONS TO SOME POLYNOMIAL CONGRUENCES IN SMALL BOXES

Part of: Diophantine equations Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  07 August 2013

IGOR E. SHPARLINSKI
IGOR E. SHPARLINSKI*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia email igor.shparlinski@mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use bounds of mixed character sum to study the distribution of solutions to certain polynomial systems of congruences modulo a prime 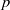$p$. In particular, we obtain nontrivial results about the number of solutions in boxes with the side length below 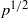${p}^{1/ 2} $, which seems to be the limit of more general methods based on the bounds of exponential sums along varieties.

Keywords

multivariate congruencesdistribution of points

MSC classification

Secondary: 11D79: Congruences in many variables 11K38: Irregularities of distribution, discrepancy
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 300 - 307
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ayyad, A., Cochrane, T. and Zheng, Z., ‘The congruence ${x}_{1} {x}_{2} \equiv {x}_{3} {x}_{4} ({\rm mod} \hspace{0.334em} p)$, the equation ${x}_{1} {x}_{2} = {x}_{3} {x}_{4} $ and the mean value of character sums’, J. Number Theory 59 (1996), 398–413.CrossRefGoogle Scholar
Boklan, K. D. and Wooley, T. D., ‘On Weyl sums for smaller exponents’, Funct. Approx. Comment. Math. 46 (2012), 91–107.Google Scholar
Chang, M.-C., ‘An estimate of incomplete mixed character sums’, in: An Irregular Mind, Bolyai Society Mathematical Studies, 21 (Springer, Berlin, 2010), 243–250.CrossRefGoogle Scholar
Fouvry, É., ‘Consequences of a result of N. Katz and G. Laumon concerning trigonometric sums’, Israel J. Math. 120 (2000), 81–96.Google Scholar
Fouvry, É. and Katz, N., ‘A general stratification theorem for exponential sums, and applications’, J. reine angew. Math. 540 (2001), 115–166.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Li, W.-C. W., Number Theory with Applications (World Scientific, Singapore, 1996).CrossRefGoogle Scholar
Luo, W., ‘Rational points on complete intersections over ${ \mathbb{F} }_{p} $’, Int. Math. Res. Not. IMRN 1999 (1999), 901–907.Google Scholar
Shparlinski, I. E., ‘On the distribution of points on multidimensional modular hyperbolas’, Proc. Japan Acad. Ser. A Math. Sci. 83 (2007), 5–9.Google Scholar
Shparlinski, I. E., ‘On a generalisation of a Lehmer problem’, Math. Z. 263 (2009), 619–631.Google Scholar
Shparlinski, I. E. and Skorobogatov, A. N., ‘Exponential sums and rational points on complete intersections’, Mathematika 37 (1990), 201–208.Google Scholar
Skorobogatov, A. N., ‘Exponential sums, the geometry of hyperplane sections, and some Diophantine problems’, Israel J. Math. 80 (1992), 359–379.Google Scholar
Weil, A., Basic Number Theory (Springer, New York, 1974).Google Scholar
Wooley, T. D., ‘Vinogradov’s mean value theorem via efficient congruencing, II’, Duke Math. J. 162 (4) (2013), 673–730.Google Scholar