Hostname: page-component-6bf8c574d5-5ws7s Total loading time: 0 Render date: 2025-03-07T03:22:07.220Z Has data issue: false hasContentIssue false
  • English
  • Français

ON STARK’S CLASS NUMBER CONJECTURE AND THE GENERALISED BRAUER–SIEGEL CONJECTURE

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  10 January 2022

PENG-JIE WONG Open the ORCID record for PENG-JIE WONG [Opens in a new window]
PENG-JIE WONG*
Affiliation:
National Center for Theoretical Sciences, No. 1, Sec. 4, Roosevelt Rd., Taipei City, Taiwan
*
e-mail: pengjie.wong@ncts.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

Stark conjectured that for any 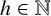$h\in \Bbb {N}$ , there are only finitely many CM-fields with class number h. Let 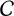$\mathcal {C}$ be the class of number fields L for which L has an almost normal subfield K such that 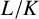$L/K$ has solvable Galois closure. We prove Stark’s conjecture for 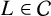$L\in \mathcal {C}$ of degree greater than or equal to 6. Moreover, we show that the generalised Brauer–Siegel conjecture is true for asymptotically good towers of number fields 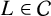$L\in \mathcal {C}$ and asymptotically bad families of 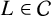$L\in \mathcal {C}$ .

Keywords

Stark’s conjectureBrauer–Siegel conjectureclass numbersasymptotically exact families

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants
Secondary: 11R42: Zeta functions and $L$-functions of number fields 11R47: Other analytic theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 288 - 300
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is currently an NCTS postdoctoral fellow.

References

Brauer, R., ‘On zeta-functions of algebraic number fields’, Amer. J. Math. 2 (1947), 243–250.CrossRefGoogle Scholar
Dixit, A. B., ‘On Euler–Kronecker constants and the generalized Brauer–Siegel theorem’, Proc. Amer. Math. Soc. 148 (2020), 1399–1414.CrossRefGoogle Scholar
Dixit, A. B., ‘On the generalized Brauer–Siegel theorem for asymptotically exact families with solvable Galois closure’, Int. Math. Res. Not. IMRN 2021 (2021), 10941–10956.CrossRefGoogle Scholar
Goldfeld, D., ‘Gauss’ class number problem for imaginary quadratic fields’, Bull. Amer. Math. Soc. (N.S.) 13 (1985), 23–37.CrossRefGoogle Scholar
Heilbronn, H. A., ‘On the class number of imaginary quadratic fields’, Q. J. Math. 5 (1934), 150–160.CrossRefGoogle Scholar
Hoffstein, J. and Jochnowitz, N., ‘On Artin’s conjecture and the class number of certain CM fields, I’, Duke Math. J. 59 (1989), 553–563.Google Scholar
Ihara, Y., ‘On the Euler–Kronecker constants of global fields and primes with small norms’, in: Algebraic Geometry and Number Theory, Progress in Mathematics, 253 (ed. Ginzberg, V.) (Birkhäuser, Boston, 2006), 407–451.CrossRefGoogle Scholar
Lagarias, J. C. and Odlyzko, A. M., ‘Effective versions of the Chebotarev density theorem’, in: Algebraic Number Fields: L-Functions and Galois properties, Proceedings of a Symposium, Durham University, Durham, 1975 (ed. Fröhlich, A.) (Academic Press, London, 1977), 409–464.Google Scholar
Louboutin, S. R., ‘Explicit upper bounds for residues of Dedekind zeta functions and values of $L$ -functions at $s=1$ , and explicit lower bounds for relative class numbers of CM-fields’, Canad. J. Math. 53 (2001), 1194–1222.CrossRefGoogle Scholar
Murty, V. K., ‘Class numbers of CM-fields with solvable normal closure’, Compos. Math. 127 (2001), 273–287.CrossRefGoogle Scholar
Odlyzko, A. M., ‘Some analytic estimates of class numbers and discriminants’, Invent. Math. 29 (1975), 275–286.CrossRefGoogle Scholar
Siegel, C. L., ‘Über die Classenzahl quadratischer Zahlkörper’, Acta Arith. 1 (1935), 83–86.CrossRefGoogle Scholar
Stark, H. M., ‘Some effective cases of the Brauer–Siegel theorem’, Invent. Math. 23 (1974), 135–152.CrossRefGoogle Scholar
Tsfasman, M. A. and Vlăduţ, S. G., ‘Infinite global fields and the generalized Brauer–Siegel theorem’, Mosc. Math. J. 2 (2002), 329–402.CrossRefGoogle Scholar
Zykin, A., ‘The Brauer–Siegel and Tsfasman–Vlăduţ theorems for almost normal extensions of number fields’, Mosc. Math. J. 5 (2005), 961–968.CrossRefGoogle Scholar