No CrossRef data available.
Article contents
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
Published online by Cambridge University Press: 24 August 2023
Abstract
Let 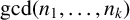 $\gcd (n_{1},\ldots ,n_{k})$ denote the greatest common divisor of positive integers
$\gcd (n_{1},\ldots ,n_{k})$ denote the greatest common divisor of positive integers  $n_{1},\ldots ,n_{k}$ and let
$n_{1},\ldots ,n_{k}$ and let 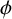 $\phi $ be the Euler totient function. For any real number
$\phi $ be the Euler totient function. For any real number 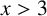 $x>3$ and any integer
$x>3$ and any integer 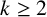 $k\geq 2$, we investigate the asymptotic behaviour of
$k\geq 2$, we investigate the asymptotic behaviour of 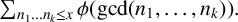 $\sum _{n_{1}\ldots n_{k}\leq x}\phi (\gcd (n_{1},\ldots ,n_{k})). $
$\sum _{n_{1}\ldots n_{k}\leq x}\phi (\gcd (n_{1},\ldots ,n_{k})). $
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author is supported by JSPS Grant-in-Aid for Scientific Research (C)(21K03205).
References
Bourgain, J., ‘Decoupling, exponential sums and the Riemann zeta-function’, J. Amer. Math. Soc. 30 (2017), 205–224.CrossRefGoogle Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums, London Mathematical Society Lecture Note Series, 126 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
Heyman, R. and Tóth, L., ‘Hyperbolic summation for functions of the GCD and LCM of several integers’, Ramanujan J., to appear. Published online (28 December 2022).CrossRefGoogle Scholar
Huxley, M. N., ‘Exponential sums and lattice points. III’, Proc. Lond. Math. Soc. (3) 87 (2003), 591–609.CrossRefGoogle Scholar
Huxley, M. N., ‘Exponential sums and the Riemann zeta-function. V’, Proc. Lond. Math. Soc. (3) 90 (2005), 1–40.CrossRefGoogle Scholar
Huxley, M. N. and Watt, N., ‘Exponential sums and the Riemann zeta-function’, Proc. Lond. Math. Soc. (3) 57 (1988), 1–24.CrossRefGoogle Scholar
Ivić, A., The Riemann Zeta-Function: Theory and Applications (Dover, Mineola, NY, 1985).Google Scholar
Kiuchi, I. and Saad Eddin, S., ‘On sums of arithmetic functions involving the greatest common divisor’, Preprint, 2021, arxiv:2102.03714v1.Google Scholar
Krätzel, E., Lattice Points, Mathematics and its Applications. East European Series, 33 (Kluwer, Dordrecht, 1988).Google Scholar
Krätzel, E., Nowak, W. G. and Tóth, L., ‘On certain arithmetic functions involving the greatest common divisor’, Cent. Eur. J. Math. 10 (2012), 761–774.Google Scholar
Kühleitner, M. and Nowak, W. G., ‘On a question of A. Schinzel: omega estimate for a special type of arithmetic functions’, Cent. Eur. J. Math. 11 (2013), 477–486.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, 163 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, revised by D. R. Heath-Brown (Oxford University Press, Oxford, 1986).Google Scholar


