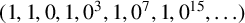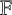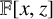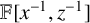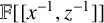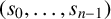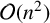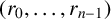ON THE BINARY SEQUENCE $(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$

Abstract

Let $\mathbb {F}$ be a field and $(s_0,\ldots ,s_{n-1})$ be a finite sequence of elements of $\mathbb {F}$. In an earlier paper [G. H. Norton, ‘On the annihilator ideal of an inverse form’, J. Appl. Algebra Engrg. Comm. Comput. 28 (2017), 31–78], we used the $\mathbb {F}[x,z]$ submodule $\mathbb {F}[x^{-1},z^{-1}]$ of Macaulay’s inverse system $\mathbb {F}[[x^{-1},z^{-1}]]$ (where z is our homogenising variable) to construct generating forms for the (homogeneous) annihilator ideal of $(s_0,\ldots ,s_{n-1})$. We also gave an $\mathcal {O}(n^2)$ algorithm to compute a special pair of generating forms of such an annihilator ideal. Here we apply this approach to the sequence r of the title. We obtain special forms generating the annihilator ideal for $(r_0,\ldots ,r_{n-1})$ without polynomial multiplication or division, so that the algorithm becomes linear. In particular, we obtain its linear complexities. We also give additional applications of this approach.

1 Introduction

The binary sequence $r=(1,1,0,1,0^3,1,0^7,1,0^{15},1,\ldots )$ has been studied by a number of authors. In [11], Rueppel conjectured that r has a perfect linear complexity profile (PLCP), that is, for any $n\geq 1$ , the linear complexity of the first n terms is $\lfloor (n+1)/2\rfloor $ . According to Dai [1, page 441], this was verified by Massey for $n=2^k-1$ and $n=2^k$ using his linear-feedback shift register (LFSR) algorithm [5]. The PLCP of this sequence was first proved in [1] by applying the Euclidean algorithm (EA) to shift-register synthesis; the essential proposition [1, Proposition 2] is proved in [2, Lemma 5]. The proof in [1] also uses an unmotivated element $\rho $ in a quadratic extension of the rational function field $\mathrm {GF}(2)(x)$ .

The continued fraction algorithm for the power series of r in $\mathrm {GF}(2)[[x^{-1}]]$ was used in [6, Corollary 2], a quadratic algorithm requiring polynomial division. We note that the methods of [4, page 439] and [3, Example 4.8] do not apply since the first $2b$ terms of the sequence are required, where b is an upper bound for the linear complexity (LC) of the sequence of length $2b$ (compare [3, Example 4.8] and [10, Example 3.7]). A derivation via the LFSR algorithm for $n=2^k$ appeared in [12, pages 46–47]. However, the derivation in [12] assumes that the ‘discrepancy’ $\Delta _n=1$ if and only if n is odd. As far as we know, the PLCP of r has not been established using the LFSR algorithm.

Let $\mathbb {F}$ be any field. Recall that the $\mathbb {F}[x,z]$ module $\mathbb {F}[[x^{-1},z^{-1}]]$ of ‘inverse series’ in variables $x^{-1},z^{-1}$ is known as Macaulay’s inverse system (in two variables, z will be our homogenising variable). Now, $\mathbb {F}[x^{-1},z^{-1}]$ is an $\mathbb {F}[x,z]$ submodule of $\mathbb {F}[[x^{-1},z^{-1}]]$ . This elementary algebraic structure underlies our approach. The sequence $(s_0,\ldots ,s_{n-1})$ has a ‘generating form’ $s_{n-1}x^{1-n}+\cdots +s_0z^{1-n}$ and hence a (homogeneous) annihilator ideal. In [8], we gave an inductive construction for the generators of such an ideal, yielding an $\mathcal {O}(n^2)$ algorithm which is easier to understand, analyse and remember than the LFSR algorithm.

Here, we specialise to $\mathbb {F}=\mathrm {GF}(2)$ and r, with $(r_{0},\ldots ,r_{9})$ and its inverse form as a running example (see Examples 4.2, 4.3). Our main results are Theorem 4.4 and linear Algorithm 4.7. We conclude by relating Theorem 4.4 to [1] and LFSRs.

Our approach is simpler and more efficient than the previous $\mathcal {O}(n^2)$ methods in the literature and: (i) it is inductive, adapting to the next term of the sequence, so we do not need all of $(r_0,\ldots ,r_{n-1})$ as in [1]; (ii) it does not use multiplication in $\mathbb {F}[x,y]$ ; (iii) we do not use the roots $\rho ,\rho ^{-1}$ of $Y^2+xY+1$ in an extension of $\mathrm {GF}(2)(x)$ as in [1]. In fact, $\rho $ arises naturally in the solution of a polynomial recurrence (Theorem 4.9); (iv) we do not assume an upper bound b on LC and $2b$ terms of the sequence as in [3, 4]; (v) unlike [6], we use no polynomial multiplications or divisions, but work with forms in $\mathbb {F}[x^{-1},z^{-1}]$ , so there are no convergence or irrationality considerations and we work with denominators only.

2 Preliminaries

We let $\mathbb {F}$ be an arbitrary field. For $f\in \mathbb {F}[x]^\times $ , we write $f^\ast $ for the reciprocal of f. We put $\mathrm {R}=\mathbb {F}[x,z]$ ; multiplication in $\mathrm {R}$ is written as juxtaposition. For $\varphi ,\varphi '\in \mathrm {R}$ and $k\in \mathbb {N}^\times $ , $x^k\,\varphi +\varphi '$ means $x^k\varphi (x,z)+\varphi '(x,z)$ and similarly for $\varphi +\,z^k\varphi '$ . The total degree of $\varphi \in \mathrm {R}^\times $ is $|\varphi |$ , with $|x|=|z|=1$ . The ideal of $\mathrm {R}$ generated by $\varphi ,\psi \in \mathrm {R}$ is written $\langle \varphi ,\psi \rangle $ .

We write $\succ $ for the graded-lexicographic order (grlex) on monomials of $\mathrm {R}^\times $ , with $|x|=|z|=1$ and $x\succ z\succ 1$ . The leading term of a form $\varphi \in \mathrm {R}$ is written $\mathrm {LT}(\varphi )$ . We define $\mathcal {L}$ to be the set of ‘leading forms’:

$$ \begin{align*}\mathcal{L}=\{\varphi\in \mathrm{R}^\times: \varphi \ \text{is a form and} \ z\nmid\mathrm{LT}(\varphi)\}.\end{align*} $$

We also use $|\ |$ for the degree function on $\mathbb {F}[x]$ , with $|0|=-\infty $ . Recall that the homogenisation of $c\in \mathbb {F}[x]^\times $ is the form $c^\wedge \in \mathrm {R}$ given by $c(x,z)=z^{|c|}c(x/z)$ and the dehomogenisation of $f\in \mathrm {R}[x,z]^\times \cap \mathcal {L}$ is $f^\vee (x)=f(x,1)\in \mathbb {F}[x]$ .

Throughout the paper, $F\in \mathrm {M}^\times =\mathbb{F}[x^{-1},z^{-1}]^\times $ denotes a typical nonzero inverse form of total degree $m=|F|\leq 0$ . We also order the monomials of $\mathrm {M}^\times $ using grlex, now written $\prec $ , but with $|x^{-1}|=|z^{-1}|=-1$ and $x^{-1}\prec z^{-1}\prec 1$ .

If F is also a form, that is, an inverse form, we write $F=\sum _{j=m}^0F_{j,m-j}x^jz^{m-j}$ ; when m is understood, we write $F_j$ for $F_{j,m-j}$ . We will use a restriction of the exponential valuation $\mathrm {v}$ for inverse forms: the order of F is

$$ \begin{align*}\mathrm{v}=\mathrm{v}(F)=\max\{j: |F|\leq j\leq 0, F_j\neq0\}. \end{align*} $$

The augmentation of F by $a\in \mathbb {F}$ is $ax^{m-1}+Fz^{-1}$ , an inverse form of total degree $m-1$ . For example, the augmentation of $z^m$ by a is $ax^{m-1}+z^{m-1}$ . A form F defines (nonzero) inverse subforms $\{F^{(j)}: m\leq j\leq \mathrm {v}\}$ by $F^{(\mathrm {v})}=x^{\mathrm {v}}$ and

$$ \begin{align*} F^{(j)}=F_jx^j+F^{(j+1)}z^{-1}=F_jx^j+\cdots +x^{\mathrm{v}} z^{j-\mathrm{v}}\quad \text{for}\ m\leq j\leq \mathrm{v}-1. \end{align*} $$

Throughout, $n\geq 1$ , $(s_0,\ldots ,s_{n-1})$ is a nonzero sequence (of elements of $\mathbb {F}$ ) and $F=F_{(s_0,\ldots ,s_{n-1})}=s_{n-1}x^{1-n}+\cdots +s_0z^{1-n}$ is the inverse form of $(s_0,\ldots ,s_{n-1})$ ; $s_{-\mathrm {v}(F)}$ corresponds to the first nonzero term of the sequence, $ax^{m-1}+Fz^{-1}$ corresponds to the augmented sequence $(s_0,\ldots ,s_{n-1},a)$ and the inverse subforms of F correspond to (nonzero) initial subsequences of $(0,\ldots ,0,s_{-\mathrm {v}(F)},\ldots ,s_{n-1})$ .

We recall the $\mathrm {R}$ submodule $\mathrm {M}=\mathbb {F}[x^{-1},z^{-1}]$ of inverse polynomials.

Definition 2.1. For nonnegative integers $p,q,u,v$ ,

(2.1) $$ \begin{align} x^pz^q\circ x^{-u}z^{-v}=\left\{\begin{array}{@{}ll} x^{p-u}z^{q-v}&\quad\text {if }p-u\leq 0, q-v\leq0,\\ 0&\quad\text{otherwise.} \end{array} \right. \end{align} $$

The $\mathrm {R}$ module structure of $\mathrm {M}$ is obtained by linearly extending (2.1) to all of $\mathrm {R}$ and $\mathrm {M}$ .

By linearity and without loss of generality, we can assume that an inverse form F satisfies $F_{\mathrm {v}}=1$ , that is, $F=F_mx^m+\cdots +F_{\mathrm {v}-1}x^{\mathrm {v}-1}z^{m-\mathrm {v}+1}+x^{\mathrm {v}} z^{m-\mathrm {v}}$ .

The annihilator ideal of an inverse form F is $\mathcal {I}_F=\{\varphi \in \mathrm {R}: \varphi \circ F=0\}$ .

Proposition 2.2 [8, Proposition 3.7].

The ideal $\mathcal {I}_F$ is homogeneous.

Proposition 2.3 [8, Lemma 3.1].

For forms $\varphi \in \mathrm {R}$ and $F\in \mathrm {M}$ with $d=|\varphi |+|F|$ either (i) $d>0$ and $\varphi \circ F=0$ or (ii)

$$ \begin{align*}\varphi\circ F=\sum _{j=d}^0[\varphi\cdot F]_j\,x^jz^{d-j}.\end{align*} $$

Thus, we trivially have $x^n\in \mathcal {I}_F$ if $n>-|F|$ .

2.1 A bijection

Next, we detail the bijection between characteristic polynomials of a sequence and the leading annihilating forms of its inverse form.

We use polynomial coefficients in their natural order, not the reversed order of ‘feedback coefficients’ and without using ‘shift registers’ as in the engineering literature. This definition enables us to exhibit a bijection between the set of ‘characteristic polynomials’ of a sequence and the leading forms of the homogeneous ideal $\mathcal {I}_F$ of $\mathrm {R}$ .

We say that $c\in \mathbb {F}[x]^\times $ is a characteristic polynomial of $(s_0,\ldots ,s_{n-1})$ if c is monic, $l=|c|$ and either: (i) $l\geq n$ or (ii)

(2.2) $$ \begin{align} c_ls_{k+l}+\cdots+c_0s_k=0\quad \text{for}\ 0\leq k\leq n-l-1 \end{align} $$

$$ \begin{align*} and\ \chi(s_0,\ldots,s_{n-1})=\{c\in\mathbb{F}[x]^\times:c \ \textit{is a characteristic polynomial of } (s_0,\ldots,s_{n-1})\}. \end{align*} $$

As $x^n$ is (vacuously) a characteristic polynomial of $(s_0,\ldots ,s_{n-1})$ , $\chi (s_0,\ldots ,s_{n-1})$ is nonempty and

$$ \begin{align*}\lambda=\lambda(s_0,\ldots,s_{n-1})=\min \{|c|:\ c\in\chi(s_0,\ldots,s_{n-1})\}\end{align*} $$

is well defined. Thus, minimal polynomials of $(s_0,\ldots ,s_{n-1})$ , that is, characteristic polynomials of minimal degree $\lambda =\lambda (s_0,\ldots ,s_{n-1})\in \mathbb {N}$ are well defined; $\lambda $ is the LC of $(s_0,\ldots ,s_{n-1})$ . We note that in [1], a characteristic polynomial of $(s_0,\ldots ,s_{n-1})$ is written $c_n$ , that is, it is indexed by the length of the sequence, not its last term.

Recall that $\mathcal {L}$ is the set of monic, leading forms in $\mathrm {R}$ , that is, $\varphi $ such that $z\nmid \mathrm {LT}(\varphi )$ . If F is an inverse form, then $x^{1-|F|}\in \mathcal {I}_F^\times \cap \mathcal {L}$ . Thus, $\mathcal {I}_F^\times \cap \mathcal {L}\neq \emptyset $ and we can consider forms in $\mathcal {I}_F^\times \cap \mathcal {L}$ of minimal total degree. So we define

$$ \begin{align*}\lambda(F)=\min\{|f|:\ f\in\mathcal{I}_F^\times\cap\mathcal{L}\}\end{align*} $$

and call $\lambda (F)$ the LC of F.

Theorem 2.4. Let $(s_0,\ldots ,s_{n-1})$ be a sequence with inverse form $F\in \mathrm {M}^\times $ . Then,

$$ \begin{align*}\wedge: \chi(s_0,\ldots,s_{n-1})\leftrightarrows \mathcal{I}_F^\times\cap \mathcal{L}: \vee\end{align*} $$

given by $\wedge (c)=c^\wedge $ and $\vee (f)=f^\vee $ are mutual, degree-preserving bijections so that for $c\in \chi (s_0,\ldots ,s_{n-1})$ , $|\wedge (c)|=|c|$ and for $f\in \mathcal {I}_F^\times \cap \mathcal {L}$ , $|\vee (f)|=|f|$ . Therefore, $\lambda (s_0,\ldots ,s_{n-1})=\lambda (F)$ .

Proof. We have $|F|=1-n$ and $|c^\wedge |=|c|=l$ . From Proposition 2.3, $c^\wedge \circ F=0$ if and only if $[c^\wedge \cdot F]_j=0$ for $l+|F|\leq j\leq 0$ . Now, $c\in \chi (s_0,\ldots ,s_{n-1})$ if and only if c satisfies (2.2), and substituting k for $-j$ , one sees that (2.2) is equivalent to $[c^\wedge \cdot F]_j=0$ for $l+|F|\leq j \leq 0$ , that is, equivalent to $c^\wedge \in \mathcal {I}_F\cap \mathcal {L}$ . So $c\in \chi (s_0,\ldots ,s_{n-1})$ if and only if $c^\wedge \in \mathcal {I}_F^\times \cap \mathcal {L}$ , we have the required bijections and hence, $\lambda (s_0,\ldots ,s_{n-1})=\lambda (F)$ .

Remark 2.5. Instead of (2.2), the LFSR algorithm uses the equivalent l and ‘connection’ polynomial $\gamma \in \mathbb {F}[x]^\times $ satisfying

$$ \begin{align*} \gamma_0s_j+\cdots+\gamma_ls_{j-l}=0\quad \text{for}\ l\leq j\leq n-1, \end{align*} $$

where $\gamma _0=1$ and $\gamma _l$ may be zero (put $j=k+l$ and $\gamma (x)=c^\ast (x)=x^l\cdot c(x^{-1})$ , the reciprocal of c, made monic). Then the LFSR synthesis algorithm returns l and $\gamma $ . Unfortunately, the formulation using reciprocal polynomials vitiates our algebraic approach.

3 Viable ordered pairs (VOPs)

3.1 The inductive construction and algorithm

We recall from [8] how to construct a ‘leading generator’ f of $\mathcal {I}_F$ in $\mathcal {L}$ which gives a minimal annihilator of F and, hence, a minimal polynomial $f^\vee $ of $(s_0,\ldots ,s_{n-1})$ . Then we give some additional properties and discuss LC profiles.

This construction is iterative, with a simple inductive basis (Proposition 3.1) and an undemanding inductive step (Theorem 3.3).

Let F be an inverse form. We say that an ordered pair of forms $(f,g)\in \mathrm {R}^2$ is a viable ordered pair (VOP) for $\mathcal {I}_F$ if:

1. (i) $f,g$ are nonzero monic forms, $f\in \mathcal {L}$ and $z \mid g$ ;

2. (ii) $\mathcal {I}_F=\langle f,g\rangle $ (we call f a leading generator and g a cogenerator of $\mathcal {I}_F$ );

3. (iii) $|f|+|g|=2-|F|$ .

Proposition 3.1 [8, Proposition 3.8].

If $F=x^m$ , then $\mathcal {I}_F=\langle x^{1-m},z\rangle $ .

The reader may check that $(f,g)=(x^{1-m},z)$ is a VOP for $\mathcal {I}_{\,x^m}$ . If $f\in \mathcal {I}_F\cap \mathcal {L}$ , we call f a leading form for $\mathcal {I}_F$ . Given a VOP $(f,g)$ for $\mathcal {I}_F$ and $G=ax^{m-1}+Fz^{-1}$ for some $a\in \mathbb {F}$ , we need to know how to construct a VOP $(\varphi ,\psi )$ for $\mathcal {I}_G$ . This requires a notion of ‘discrepancy’ that shows how a and $\mathcal {I}_F$ affect $\mathcal {I}_G$ . It is our analogue of ‘discrepancy’ introduced in [5]; it is the obstruction to extending f to a leading form of $\mathcal {I}_G$ .

Definition 3.2. If $f\in \mathcal {I}_F^\times $ is a form and $G= ax^{m-1}+z^{-1}F$ , then the discrepancy $\Delta (f;G)$ of f and G is 0 if $|f|+|G|>0$ and $[f\cdot G]_{(|f|+|G|,0)}\in \mathbb {F}$ otherwise.

The inductive step is given by the following result.

Theorem 3.3 [8, Proposition 4.6, Theorem 4.12].

Let $(f,g)$ be a VOP for $\mathcal {I}_F$ , $a\in \mathbb {F}$ and $G=ax^{|F|-1}+Fz^{-1}$ . Suppose that $g\not \in \mathcal {I}_G$ and put $\Delta '=\Delta (g;G)\in \mathbb {F}^\times $ , $d=|g|-|f|$ , $\Delta =\Delta (f;G)\in \mathbb {F}$ . If $\Delta =0$ , set $(\varphi ,\psi )=(f,zg)$ and $d=d+1$ . However, if $\Delta \neq 0$ , put $q=\Delta /\Delta '$ and

$$ \begin{align*} (\varphi,\psi)=\left\{\begin{array}{@{}ll} (f-q\,x^{-d}g,z\,g)&\quad\text {if } d\leq0,\\ (x^{+d}f-q\,g,zf)&\quad\text{otherwise.} \end{array} \right. \end{align*} $$

Then, $(\varphi ,\psi )$ is a VOP for G and manifestly $|\varphi |=|f|$ if $d\leq 0$ and $|\varphi |=|g|$ otherwise. In particular, $|\varphi |=\max \{|g|,|f|\}$ .

For the next iteration:

1. (i) $e=|\psi |-|\varphi |=1$ if $\Delta =0$ and $e=1-|d|$ if $\Delta \neq 0$ ;

2. (ii) if $d>0$ , $b\in \mathbb {F}$ and $\Delta (\varphi ;b\,x^{|G|-1}+Gz^{-1})\neq 0$ , we put $\Delta '=\Delta $ , otherwise $\Delta '$ is unchanged.

Proposition 3.4 [8, Proposition 3.5].

If $(f,g)$ is a VOP for F, then $\lambda (F)=|f|$ .

We will often write $d_k=|g^{(k)}|-|f^{(k)}|$ and $\Delta _k=\Delta (f^{(k)};F^{(-k-1)})$ . We will refer to $x^{d_k}$ (if $\Delta _k\neq 0\ \text {and}\ \ d_k>0)$ and $x^{-d_k}$ (if $\Delta _k\neq 0\ \text {and}\ d_k\leq 0)$ as the intermediate shifts in the construction. The following $\mathcal {O}(m^2)$ algorithm is based on Theorem 3.3.

Algorithm 3.5 (VOP)

We note that homogenising $(\mu ,\nu )\in \mathbb {F}[x]^2$ of [7] also yields a VOP (see [8, Theorem 6.15]).

3.2 Some additional properties

If $F=x^m$ , then $\mathcal {I}_F=\langle x^{1-m},z\rangle $ by Proposition 3.1 and $\gcd (x^{1-m},z)=1$ . The next result shows that a VOP $(f,g)$ always satisfies $\gcd (f,g)=1$ .

Proposition 3.6. If $(f,g)$ is a VOP for $\mathcal {I}_F$ , $\gcd (f,g)=1$ and $\varphi ,\psi $ are as constructed, then $\gcd (\varphi ,\psi )=1$ .

Proof. If $\Delta =0$ and $h \mid \gcd (f,zg)$ , then $h=z$ or $h \mid g$ . However, if $z \mid f$ , then $z \mid \mathrm {LT}(f)$ which is impossible, so $h \mid \gcd (f,g)$ . Suppose that $\Delta \neq 0$ and $d\leq 0$ . Then, $\gcd (\varphi ,\psi )=\gcd (f,zg)=\gcd (f,g)=1$ as before. However, suppose that $d>0$ . If $h \mid zf$ and $h \mid g$ , then either: (i) $h=z$ and $h \mid \varphi $ or (ii) $h \mid f$ and $h \mid (x^df-q\,g)$ . However, item (i) is impossible since $z\nmid \mathrm {LT}(\varphi )$ so item (ii) is obtained and $h \mid \gcd (f,g)=1$ .

We know that $(x^{1-m},z)$ is a VOP for $\mathcal {I}_F$ and $x^{1-m}$ is a leading form of minimal degree. However, so is $x^{1-m}+\varphi \,z$ for any form with $|\varphi |=-m$ . More generally, we have the following result.

Corollary 3.7 (Compare [6, Theorem 1]).

Let $\Theta {\kern-1pt}={\kern-1pt}\Theta _F{\kern-1pt}={\kern-1pt}\{\theta {\kern-1pt}\in{\kern-1pt} \mathcal {I}_F{\kern-1pt}\cap{\kern-1pt} \mathcal {L} {\kern-1pt}:{\kern-2pt}\ |\theta\kern0.2pt |\ is\ minimal\}$ . If $(f,g)$ is a VOP for $\mathcal {I}_F$ , then

$$ \begin{align*}\Theta=\left\{\begin{array}{@{}ll} \{ f\} & \quad\text{if}\ |g|>|f|,\\ \{ f\}\cup\{ f+\psi\cdot g: \psi\ \text{is a form and}\ |\psi|=|f|-|g|\} & \quad\text{otherwise.} \end{array} \right. \end{align*} $$

Proof. If $|g|>|f|$ and then f is the only monic leading annihilating form of minimal degree $|f|$ since $\mathcal {I}_F=\langle f,g\rangle $ . However, if $|g|\leq |f|$ and $\psi \in \mathrm {R}^\times $ is a form with ${|\psi |=|f|-|g|}$ , then $h=f+\psi \cdot g\in \mathcal {I}_F$ is a monic leading form since $\mathrm {LT}(h)=\mathrm {LT}(f)$ and $|h|=|f|$ is minimal.

In [8, Example 4.24], we obtained $(f,g)=(x^4+x^3z+x^2z^2,x^3z+x^2z^2+xz^3+z^4)$ for the inverse form $F=x^{-6}+x^{-4}z^{-2}+x^{-3}z^{-3}+z^{-6}$ . Here, $f(0,1)=0$ . However, $h=f+g\in \mathcal {I}_F$ satisfies $h(0,1)=1$ . (In fact, $h\in \mathcal {I}_{z^{-1}F}$ .)

More generally, if we have an inverse form F and begin iterating with $(x^{1-|F|},z)$ , then the construction provides a VOP $(f,g)$ with $\gcd (f,g)=1$ . Hence, if $f(a,b)=0$ for some $a,b\in \mathbb {F}$ , then $g(a,b)\neq 0$ and if $|g|\leq |f|$ , then $h=f+x^{|f|-|g|}g$ is a leading form in $\mathcal {I}_F$ such that $h(a,b)\neq 0$ . However, if $|g|> |f|$ , then $h=x^{|g|-|f|}f+g\in \mathcal {I}_F$ is a leading form such that $h(a,b)\neq 0$ , but of increased degree $|g|$ .

3.3 LC profiles

An inverse form F has subforms $F^{(j)}$ for $m=|F|\leq j\leq \mathrm {v}=\mathrm {v}(F)$ , with $F^{(\mathrm {v})}=x^{\mathrm {v}}$ and $F^{(m)}=F$ . We write $\lambda (F^{(j)})$ for the LC of the subform $F^{(j)}$ .

We call the sequence $(\lambda (F^{(\mathrm {v})}),\ldots , \lambda (F^{(m)}))$ of integers the LC profile of F and say that F has a PLCP if $\mathrm {v}=0$ and $\lambda (F^{(-k)})=\lfloor (k+1)/2\rfloor $ for $0\leq k\leq -m$ . From Theorem 2.3, this agrees with the usual notion of the LC profile of a sequence. Next we relate the notion of PLCP to the intermediate shifts occurring in Theorem 3.3.

Proposition 3.8. Let F be an inverse form with $F_0=1$ . For $1\leq k<-m$ , let $(f^{(k)},g^{(k)})$ be a VOP for $\mathcal {I}_{F^{(-k)}}$ and $F^{(-1-k)}$ be the $(-1-k)$ th subform of F. Put $\Delta _k=\Delta (f^{(k)};F^{(-1-k)})$ . The following are equivalent:

1. (i) F has a PLCP;

2. (ii) the intermediate shift is x if and only if k is odd.

Proof. The quantity $\lfloor (k+1)/2\rfloor $ is 1 for $k=1$ , and increases by 1 if and only if k is odd. Since $F_0=1$ , $(f^{(0)},g^{(0)})=(x,z)$ , that is, $|f^{(0)}|=1$ and $d_0=0$ . Thus, either $(f^{(1)},g^{(1)})=(x,z^2)$ or $(f^{(1)},g^{(1)})=(x-z,z^2)$ . Next, the degree $|f^{(k)}|$ increases by 1 if and only if k is odd, and is equivalent to $f^{(k+1)}=xf^{(k)}-q_k g^{(k)}$ if k is odd and $f^{(k+1)} =f^{(k)}-q_k g^{(k)}$ if k is even.

Proposition 3.8 is an analogue of [6, Theorem 2] without an irrationality hypothesis and our intermediate shifts are analogous to the partial quotients of [6].

Moreover, $\Delta _k$ is arbitrary when k is even. The average LC of a random binary $(s_0,\ldots ,s_{n-1})$ is $n/2+a_n$ , where $0\leq a_n\leq 5/18$ [12, Ch. 4]. Thus, a binary sequence with $s_0=1$ and $s_i$ chosen so that $\Delta _k=1$ when k is odd and randomly when k is even will: (i) have a PLCP and (ii) be a good approximation to a random binary sequence.

4 The sequence r and its inverse forms

From now on, $\mathbb {F}=\mathrm {GF}(2)$ and $r=(1,1,0,1,0^3,1,0^7,1,0^{15},1,\ldots )$ , where $r_i=1\in \mathbb {F}$ if $i=2^k-1$ for some $k\geq 0$ and $r_i=0$ otherwise.

Definition 4.1. For $n\geq 1$ , the inverse form of $(r_0,\ldots ,r_{n-1})$ is

$$ \begin{align*}R^{(1-n)}=R^{(1-n)}(x^{-1},z^{-1})=\sum_{j=1-n}^0 r_{-j}x^jz^{1-n-j}\in\mathbb{F}[x^{-1},z^{-1}].\end{align*} $$

We write $\mathcal {I}_{n-1}$ for $\mathcal {I}_{R^{(1-n)}}$ . Note that $R^{(1-n)}$ and $\mathcal {I}_{n-1}$ are indexed using the last index of $(r_0,\ldots ,r_{n-1})$ rather than the length of the sequence. We have $|R^{(1-n)}|=1-n$ , $R^{(1-2^k)}=\sum _{j=k}^0 x^{1-2^j}z^{2^j-2^k}$ for $k\geq 0$ , and if $k\geq 1$ , then $R^{(1-2^k)}=x^{1-2^k}+R^{(1-2^{k-1})}z^{-2^{k-1}}$ . In addition, if $2^k-1<n<2^{k+1}-1$ , then $R^{(-n)}=R^{(1-2^k)}z^{2^k-1-n}\in z^{-1}\mathrm {M}$ .

Example 4.2. The inverse forms $R^{(j)}$ for $-9\leq j\leq 0$ are given in Table 1.

Recall that $\Delta _{k-1}=\Delta (f^{(k-1)};R^{(-k)})=[f^{(k-1)}\cdot R^{(-k)}]_{(|f^{(k-1)}|-k,0)}$ and $q_{k-1}=\Delta _{k-1}$ for $0\leq k-1\leq n-1$ .

Example 4.3 (Example 4.2 continued).

Since $R^{(0)}=1$ , $\mathcal {I}_0=\langle f^{(0)},g^{(0)}\rangle =\langle x,z\rangle $ from Proposition 3.1. However, we can and will take $(f^{(0)},g^{(0)})=(x+z,z)$ so that $f^{(0)}(0,1)=1$ . The key ingredients for the construction are the degree increment $d_{k}=|g^{(k)}|-|f^{(k)}|$ and the discrepancy $\Delta _k$ , so that we know how to update $(f^{(k)},g^{(k)})$ . We obtain the results shown in Table 2. For $0\leq k\leq 9$ , $f^{(k)}=\lfloor (k+2)/2\rfloor =\lambda _{k+1}$ (recall that $f^{(k)}\circ (r_0,\ldots ,r_k)=0$ where there are $k+1$ terms of r). From Corollary 3.7, $f^{(k)}$ is the unique leading annihilating form of minimal total degree if k is odd and $f^{(k)}+g^{(k)}$ is the only other leading annihilating form of minimal total degree when k is even.

The significance of the underlined terms will become clear in the proof of Theorem 4.4.

We now come to our main result.

Theorem 4.4. Let $(f^{(0)},g^{(0)})=(x+z,z)$ and for $k\geq 0$ , let $(f^{(k+1)},g^{(k+1)})$ be as constructed in Theorem 3.3.

1. (A) If k is even, then $\Delta _k=0$ ; otherwise, $\Delta _k=1$ and $d_k=1$ .

2. (B) We have

   $$ \begin{align*} (f^{(k+1)},g^{(k+1)})=\left\{\begin{array}{@{}ll} (f^{(k)},zg^{(k)})&\quad\text {if } \ k\ \text{is even},\\ (xf^{(k)}+g^{(k)},zf^{(k)})&\quad\text{otherwise}. \end{array} \right. \end{align*} $$

3. (C) $|f^{(k+1)}|=\lfloor (k+3)/2\rfloor $ .

4. (D) $f^{(k+1)}(0,1)=g^{(k+1)}(0,1)=1$ .

Proof. We have $(f^{(0)},g^{(0)})=(x+z,z)$ , where $\Delta _0=0$ , $|f^{(0)}|=1=\lfloor 2/2\rfloor $ and $f^{(0)}(0,1)=1=g^{(0)}(0,1)$ . Suppose inductively that the result is true for k.

Table 1 Inverse forms $R^{(j)}$ for Example 4.2.

Table 2 Calculations for the VOP algorithm for Example 4.2.

(A) For $f^{(k+1)}$ , we have to determine $\Delta _k=[f^{(k)}\cdot R^{(-1-k)}]_{(|f^{(k)}|-1-k,0)}$ . Let $P=2^p-1\leq k+1<2^{p+1}-1$ for some $p\geq 1$ . Put $e=|f^{(k)}|$ and $l=e-1-k$ . Then,

$$ \begin{align*}S=R^{(-1-k)}=\bigg(\sum_{j=p}^0 x^{1-2^j}z^{2^j-2^p}\bigg)z^{P-1-k}\quad \text{and}\quad \Delta_k=[f^{(k)}\cdot S]_{(l,0)}.\end{align*} $$

We consider three cases.

Case (i): k even, $P=k+1$ . We have to show that $\Delta _k=0$ . Since $k-1$ is odd, the inductive hypothesis gives $\Delta _{k-1}=1$ , $d_{k-1}=1$ and $(f^{(k)},g^{(k)})=(xf^{(k-1)}+g^{(k-1)}, zf^{(k-1)})$ . Also, $|f^{(k)}|=|f^{(k-1)}|+1= k/2+1=2^{p-1}$ , so $l=|f^{(k)}|-k-1=2^{p-1}+1-2^p= 1-2^{p-1}$ . By part (A), $f^{(k)}(0,1)=1$ , so we can write $f^{(k)}\cdot S$ as

$$ \begin{align*} (x^e+\alpha+z^e)\cdot (x^{1-2^p}+x^{1-2^{p-1}}z^{-2^{p-1}}+\beta). \end{align*} $$

Then $x^e\cdot x^{1-2^p}=x^l$ , and one checks that $(\alpha +z^e)\cdot (x^{1-2^{p-1}}z^{-2^{p-1}}+\beta )=x^l$ plus terms in $z^{-1}\mathrm {M}$ , so $\Delta _k=[f^{(k)}\cdot S]_{(l,0)}=0$ and $f^{(k+1)}=f^{(k)}$ .

Case (ii): k even, $P<k+1<2^{p+1}-1$ . Here, $P-k-1<0$ and $S\in z^{-1}\mathrm {M}$ . As in case (i), $(f^{(k)},g^{(k)})=(xf^{(k-1)}+g^{(k-1)},zf^{(k-1)})$ and $e=|f^{(k)}|=|f^{(k-1)}|=2^{p-1}$ . Then,

$$ \begin{align*}f^{(k)}\cdot S=(x^e+(f^{(k)}+x^e))\cdot R^{(-P)}z^{P-k-1}.\end{align*} $$

However, $x^e\cdot R^{(-P)}z^{P-k-1}$ , $(f^{(k)}+x^e)\cdot x^{-P}$ , $(f^{(k)}+x^e)\cdot (R^{(-P)}+x^{-P})z^{P-k-1}\in z^{-1}\mathrm {M}$ , so $\Delta _k=0$ and again $f^{(k+1)}=f^{(k)}$ .

Case (iii): k odd and $P\hspace{-1pt}\leq\hspace{-1pt} k\hspace{-1pt}<\hspace{-1pt}2^{p+1}\hspace{-1pt}-\hspace{-1pt}1$ . For $k\hspace{-1pt}=\hspace{-1pt}1$ , $\Delta _1\hspace{-1pt}=\hspace{-1pt}[(x\hspace{-1pt}+\hspace{-1pt}\underline {z})\cdot (x^{-1}z^{-1}\hspace{-1pt}+\hspace{-1pt}z^{-2})]_{(1-2,0)}\hspace{-1pt}=\hspace{-1pt}1$ ; the term $\underline {z}$ of $f^{(1)}$ has triggered $\Delta _1=1$ . The reader may easily verify that $\underline {xz}=\alpha z$ triggers $\Delta _3=1$ and that $\underline {z}^3=\beta z$ triggers $\Delta _5=1$ . Now let k be odd and $p\geq 3$ , $P=2^p-1\leq k<2^{p+1}-1$ . Define maps $\alpha ,\beta :\mathrm {R}\rightarrow \mathrm {R}$ by $(\alpha \ f)(x,z)=x\cdot f(x,z)$ and $(\beta \ f)(x,z)=z^2\cdot f(x,z)$ . Since $k-1$ is even, the inductive hypothesis gives

$$ \begin{align*}f^{(k)}=f^{(k-1)}=xf^{(k-2)}+ g^{(k-2)}=\alpha\ f^{(k-2)}+ \beta\ f^{(k-4)},\end{align*} $$

$e=|f^{(k)}|=|f^{(k-1)}|=(k+1)/2$ and $l=e+|S|=(k+1)/2-1-k=-(k+1)/2$ .

Put $t_k= x^{u_k}z^{v_k}$ , where $u_k=P-{(k+1)}/{2}$ , $v_k=k+1-P$ . Then, $|t_k|=(k+1)/2=|f^{(k)}|$ and $t_k=\alpha ^{u_k}\beta ^{(v_k-1)/2}z$ . Since z is a term of $f^{(1)}$ , $t_k$ is a term of $f^{(2u_k+2v_k-1)}=f^{(k)}$ .

Let $L=\mathrm {LT}(S)$ , where $S=R^{(-P)}z^{P-k-1}\in z^{-1}\mathrm {M}$ . Then,

$$ \begin{align*} f^{(k)}\cdot S=f^{(k)}\cdot (L+S)+f^{(k)}\cdot L=f^{(k)}\cdot (L+S)+t_k\cdot L+(f^{(k)}+t_k)\cdot L \end{align*} $$

and $t_k\cdot L=x^{(k-1)/2}z\cdot x^{-k}z^{-1}=x^l$ . It is straightforward that $f^{(k)}\cdot (L+S)\in z^{-1}\mathrm {M}$ and $(f^{(k)}+t_k)\cdot L\in z^{-1}\mathrm {M}$ . Thus, $\Delta _k=[f^{(k)}\cdot S]_{(l,0)}=[t_k\cdot L]_{(l,0)}=1$ , the term $t_k$ of $f^{(k)}$ triggers $\Delta _k=1$ and $(f^{(k+1)},g^{(k+1)}) =(xf^{(k)}+g^{(k)},zf^{(k)})$ .

(B) This is a simple consequence of part (A).

(C) Suppose that $|f^{(k)}|=\lfloor (k+2)/2\rfloor $ . From part (B), if k is even, then $|f^{(k+1)}|=|f^{(k)}|=(k+2)/2=\lfloor (k+3)/2\rfloor $ and if k is odd, then $|f^{(k+1)}|=|f^{(k)}|+1=\lfloor (k+2)/2\rfloor +1=(k+1)/2+1=(k+3)/2=\lfloor (k+3)/2\rfloor $ .

(D) We know that $f^{(k)}(0,1)=g^{(k)}(0,1)=1$ for $k=0,1$ , so suppose that the result is true for k. If k is even, $f^{(k+1)}(0,1)=f^{(k)}(0,1)=1$ and $g^{(k+1)}(0,1)=1$ , whereas if k is odd, $f^{(k+1)}(0,1)=g^{(k)}(0,1)=1$ and $g^{(k+1)}(0,1)=f^{(k)}(0,1)=1$ .

Remark 4.5. In Example 4.3, the underlined terms trigger a discrepancy of 1: for odd k and $2^p-1\leq k< 2^{p+1}-1$ , $u_{k+1}=u_k-1$ , $v_{k+2}=v_k+2$ , so that the $t_k$ in the proof of Theorem 4.4 take the values $x^pz^1,x^{p-1}z^3,x^{p-2}z^5, \ldots , x^0z^{2^p-1}$ .

The next result is immediate from Proposition 3.8, Theorem 4.4 and Corollary 3.7.

Corollary 4.6.

1. (i) The sequence $(r_0,r_1,\ldots )$ has a PLCP.

2. (ii) If n is odd, $(r_0,\ldots ,r_{n-1})$ has a unique leading form of minimal degree, namely $f^{(n-2)}$ , or the leading forms of minimal degree are precisely the two forms $f^{(n-2)}$ and $f^{(n-2)}+g^{(n-2)}$ .

From Theorem 4.4, no multiplications in $\mathrm {R}$ are required to compute a VOP, giving the following linear algorithm.

Algorithm 4.7 (VOP algorithm specialised to $R^ {(1-n)}$ ).

For additional properties of $\mathcal {I}_{n-1}$ , for example, its codimension and how to compute its (unique) reduced grlex Groebner basis, see [8, Corollary 5.18, Algorithm 5.24] and [9, Section 4].

4.1 Relating Theorem 4.4 to [1] and LFSRs

We next give a closed-form expression for $f^{(2k-1)}$ dehomogenised; this also motivates the use of the roots $Y^2+xY+1$ in an extension of $\mathbb {F}(x)$ , which were unmotivated in [1].

Lemma 4.8. Let $h^{(k)}\in \mathbb {F}[x]$ be given by $h^{(0)}=x$ , $h^{(1)}=x+1$ , $h^{(2)}=x^2+x+1$ and $h^{(k)}=x\,h^{(k-1)}+h^{(k-2)}$ for $k\geq 3$ . Then,

$$ \begin{align*}x\, h^{(k)}= (1+\rho)\rho^k+(1+\rho^{-1})\rho^{-k},\end{align*} $$

where $\rho =\overline {Y}\in \mathbb {F}(x)[Y]/(Y^2+xY+1)=\mathbb {K}$ .

Proof. The given recurrence has characteristic polynomial $Y^2+xY+1\in \mathbb {F}(x)[Y]$ , which is irreducible. (One easily shows that if $Y^2+xY+1=(Y+u)(Y+v)$ for some $u,v\in \mathbb {F}(x)$ , then $x=0$ .) So let $\rho =\overline {Y}\in \mathbb {K}$ . Solving $h^{(k)}=A\rho ^k+B\rho ^{-k}$ for $A,B\in \mathbb {F}(x)$ subject to $h^{(1)}=x+1$ , $h^{(2)}=x^2+x+1$ gives the required expression.

We note that the $2\times 2$ matrix $(\begin {smallmatrix} 1&0\\ 0&x \end {smallmatrix})$ much used in [1] has characteristic polynomial $Y^2+xY+1$ .

We now set $\rho =\overline {Y}\in \mathbb {F}(x)[Y]/(Y^2+xY+1)$ .

Theorem 4.9. For $k\geq 1$ , $x\,f^{(2k-2)}(x,1)=x\,f^{(2k-1)}(x,1)=(1+\rho )\rho ^k+(1+\rho ^{-1})\rho ^{-k}.$

Proof. Theorem 4.4 implies that we may take $h^{(k)}=f^{(2k-2)}(x,1)$ in Lemma 4.8; $f^{(2k-2)}=f^{(2k-1)}$ and $|g^{(2k-1)}|=|f^{(2k-1)}|+1$ , so $f^{(2k-1)}$ is unique.

Corollary 4.10 (See [1, Lemma 5]).

Let $\eta =(1+\rho )\rho ^k+(1+\rho ^{-1})\rho ^{-k}\in \mathbb {K}$ as in Lemma 4.8. Then, $\eta \in \mathbb {F}[x]$ , $x \mid \eta $ and $|\eta |=k+1$ .

Corollary 4.11. For $k\geq 1$ , let $c_k$ be the minimal polynomial for $(r_0,\ldots ,r_{2k-1})$ as in [1]. Then, $c_k(x)=f^{(2k-1)}(x,1)$ .

Proof. Reference [1, Lemma 3] implies that $c_k$ satisfies the recurrence of Lemma 4.8.

Corollary 4.12. The LFSR algorithm applied to $(r_0,\ldots ,r_{2k-1})$ returns k and the reciprocal polynomial $f^{(2k-1)}(x,1)^\ast $ .

Proof. From Remark 2.5 and Theorem 4.4, $|f^{(2k-1)}(x,{\kern-1pt}1)|{\kern-1pt}={\kern-1pt}k$ and $f^{(2k-1)}(0,{\kern-1pt}1){\kern-1pt}={\kern-1pt}1$ .