Article contents
ON THE BRÜCK CONJECTURE
Published online by Cambridge University Press: 02 October 2015
Abstract
The Brück conjecture states that if a nonconstant entire function 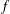 $f$ with hyper-order
$f$ with hyper-order 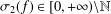 ${\it\sigma}_{2}(f)\in [0,+\infty )\setminus \mathbb{N}$ shares one finite value
${\it\sigma}_{2}(f)\in [0,+\infty )\setminus \mathbb{N}$ shares one finite value  $a$ (counting multiplicities) with its derivative
$a$ (counting multiplicities) with its derivative 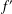 $f^{\prime }$, then
$f^{\prime }$, then 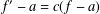 $f^{\prime }-a=c(f-a)$, where
$f^{\prime }-a=c(f-a)$, where  $c$ is a nonzero constant. The conjecture has been established for entire functions with order
$c$ is a nonzero constant. The conjecture has been established for entire functions with order 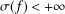 ${\it\sigma}(f)<+\infty$ and hyper-order
${\it\sigma}(f)<+\infty$ and hyper-order 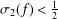 ${\it\sigma}_{2}(f)<{\textstyle \frac{1}{2}}$. The purpose of this paper is to prove the Brück conjecture for the case
${\it\sigma}_{2}(f)<{\textstyle \frac{1}{2}}$. The purpose of this paper is to prove the Brück conjecture for the case 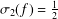 ${\it\sigma}_{2}(f)=\frac{1}{2}$ by studying the infinite hyper-order solutions of the linear differential equations
${\it\sigma}_{2}(f)=\frac{1}{2}$ by studying the infinite hyper-order solutions of the linear differential equations 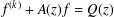 $f^{(k)}+A(z)f=Q(z)$. The shared value
$f^{(k)}+A(z)f=Q(z)$. The shared value  $a$ is extended to be a ‘small’ function with respect to the entire function
$a$ is extended to be a ‘small’ function with respect to the entire function 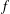 $f$.
$f$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
- 9
- Cited by

