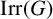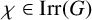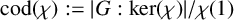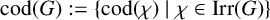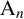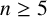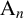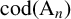1 Introduction
Let G be a finite group and
![]() $\mathrm {Irr}(G)$
the set of all irreducible complex characters of G. For any
$\mathrm {Irr}(G)$
the set of all irreducible complex characters of G. For any
![]() $\chi \in \mathrm {Irr}(G),$
define the codegree of
$\chi \in \mathrm {Irr}(G),$
define the codegree of
![]() $\chi $
as
$\chi $
as
![]() $\mathrm {cod}(\chi ) := {|G:\mathrm {ker}(\chi )|}/{\chi (1)}$
and the codegree set of G as
$\mathrm {cod}(\chi ) := {|G:\mathrm {ker}(\chi )|}/{\chi (1)}$
and the codegree set of G as
![]() $\mathrm {cod}(G) := \{\mathrm {cod}(\chi ) \mid \chi \in \mathrm {Irr}(G)\}.$
We refer the reader to the authors’ previous paper [Reference Dolorfino, Martin, Slonim, Sun and Yang8] for the current literature on codegrees.
$\mathrm {cod}(G) := \{\mathrm {cod}(\chi ) \mid \chi \in \mathrm {Irr}(G)\}.$
We refer the reader to the authors’ previous paper [Reference Dolorfino, Martin, Slonim, Sun and Yang8] for the current literature on codegrees.
The following conjecture appears in the Kourovka Notebook of Unsolved Problems in Group Theory [Reference Khukrho and Mazurov12, Question 20.79].
Codegree Version of Huppert’s Conjecture. Let H be a finite nonabelian simple group and G a finite group such that
![]() $\mathrm {cod}(H) = \mathrm {cod}(G).$
Then
$\mathrm {cod}(H) = \mathrm {cod}(G).$
Then
![]() $G \cong H$
.
$G \cong H$
.
In [Reference Dolorfino, Martin, Slonim, Sun and Yang8], the authors verified the conjecture for all sporadic simple groups. In this paper, we provide a general proof verifying this conjecture for all alternating groups of degree greater than or equal to
![]() $5$
.
$5$
.
Theorem 1.1. Let
![]() $\mathrm {A}_n$
be an alternating group of degree
$\mathrm {A}_n$
be an alternating group of degree
![]() $n \ge 5$
and G a finite group. If
$n \ge 5$
and G a finite group. If
![]() $\mathrm {cod}(G)= \mathrm {cod}(\mathrm {A}_n)$
, then
$\mathrm {cod}(G)= \mathrm {cod}(\mathrm {A}_n)$
, then
![]() $G \cong \mathrm {A}_n$
.
$G \cong \mathrm {A}_n$
.
Throughout the paper, we follow the notation used in Isaacs’ book [Reference Isaacs10] and the ATLAS of Finite Groups [Reference Conway, Curtis, Norton, Parker and Wilson6].
2 Proof of Theorem 1.1
First, we note that the cases
![]() $n=5,6$
and
$n=5,6$
and
![]() $7$
have already been proven in [Reference Ahanjideh1, Reference Bahri, Akhlaghi and Khosravi2], so in the following, we always assume that
$7$
have already been proven in [Reference Ahanjideh1, Reference Bahri, Akhlaghi and Khosravi2], so in the following, we always assume that
![]() $n>7.$
Now, let G be a minimal counterexample and N be a maximal normal subgroup of G. So
$n>7.$
Now, let G be a minimal counterexample and N be a maximal normal subgroup of G. So
![]() $\mathrm {cod}(G)=\mathrm {cod}(\mathrm {A}_n)$
and
$\mathrm {cod}(G)=\mathrm {cod}(\mathrm {A}_n)$
and
![]() $G/N$
is simple. By [Reference Dolorfino, Martin, Slonim, Sun and Yang8, Lemma 2.5],
$G/N$
is simple. By [Reference Dolorfino, Martin, Slonim, Sun and Yang8, Lemma 2.5],
![]() $\mathrm {cod}(G/N)\subseteq \mathrm {cod}(\mathrm {A}_n)$
. Then, by [Reference Hung and Moreto9, Theorem B],
$\mathrm {cod}(G/N)\subseteq \mathrm {cod}(\mathrm {A}_n)$
. Then, by [Reference Hung and Moreto9, Theorem B],
![]() $G/N\cong \mathrm {A}_n$
so
$G/N\cong \mathrm {A}_n$
so
![]() $N\neq 1$
since
$N\neq 1$
since
![]() $G\not \cong \mathrm {A}_n$
.
$G\not \cong \mathrm {A}_n$
.
Step 1: N is a minimal normal subgroup of G.
Suppose L is a nontrivial normal subgroup of G with
![]() $L < N$
. Then by [Reference Dolorfino, Martin, Slonim, Sun and Yang8, Lemma 2.6],
$L < N$
. Then by [Reference Dolorfino, Martin, Slonim, Sun and Yang8, Lemma 2.6],
![]() $\mathrm {cod}(G/N) \kern1.3pt{\subseteq}\kern1.3pt \mathrm {cod}(G/L) \kern1.3pt{\subseteq}\kern1.3pt \mathrm {cod}(G)$
. However,
$\mathrm {cod}(G/N) \kern1.3pt{\subseteq}\kern1.3pt \mathrm {cod}(G/L) \kern1.3pt{\subseteq}\kern1.3pt \mathrm {cod}(G)$
. However,
![]() ${\mathrm {cod}(G/N)\kern1.3pt{=}\kern1.3pt\mathrm {cod}(\mathrm {A}_n)\kern1.3pt{=}\kern1.3pt\mathrm {cod}(G)}$
, so equality must be attained in each inclusion. Thus,
${\mathrm {cod}(G/N)\kern1.3pt{=}\kern1.3pt\mathrm {cod}(\mathrm {A}_n)\kern1.3pt{=}\kern1.3pt\mathrm {cod}(G)}$
, so equality must be attained in each inclusion. Thus,
![]() $\mathrm {cod}(G/L)=\mathrm {cod}(\mathrm {A}_n)$
which implies that
$\mathrm {cod}(G/L)=\mathrm {cod}(\mathrm {A}_n)$
which implies that
![]() $G/L \cong \mathrm {A}_n$
since G is a minimal counterexample. This is a contradiction since we also have
$G/L \cong \mathrm {A}_n$
since G is a minimal counterexample. This is a contradiction since we also have
![]() $G/N\cong \mathrm {A}_n,$
but
$G/N\cong \mathrm {A}_n,$
but
![]() $L < N$
.
$L < N$
.
Step 2: N is the only nontrivial, proper normal subgroup of G.
Otherwise, we assume M is another proper nontrivial normal subgroup of G. If N is included in M, then
![]() $M=N$
or
$M=N$
or
![]() $M=G$
since
$M=G$
since
![]() $G/N$
is simple, which is a contradiction. Then
$G/N$
is simple, which is a contradiction. Then
![]() $N\cap M=1$
and
$N\cap M=1$
and
![]() $G=N\times M$
. Since M is also a maximal normal subgroup of G, we have
$G=N\times M$
. Since M is also a maximal normal subgroup of G, we have
![]() $N\cong M\cong \mathrm {A}_n$
. Choose
$N\cong M\cong \mathrm {A}_n$
. Choose
![]() $\psi _1\in \operatorname {Irr}(N)$
and
$\psi _1\in \operatorname {Irr}(N)$
and
![]() $\psi _2\in \operatorname {Irr}(M)$
such that
$\psi _2\in \operatorname {Irr}(M)$
such that
![]() $\operatorname {cod}(\psi _1)=\operatorname {cod}(\psi _2)=\max (\operatorname {cod}(\mathrm {A}_n))$
. Set
$\operatorname {cod}(\psi _1)=\operatorname {cod}(\psi _2)=\max (\operatorname {cod}(\mathrm {A}_n))$
. Set
![]() $\chi =\psi _1\cdot \psi _2\in \operatorname {Irr}(G)$
. Then
$\chi =\psi _1\cdot \psi _2\in \operatorname {Irr}(G)$
. Then
![]() $\operatorname {cod}(\chi )=(\max (\operatorname {cod}(\mathrm {A}_n)))^2\notin \operatorname {cod}(G)$
, which is a contradiction.
$\operatorname {cod}(\chi )=(\max (\operatorname {cod}(\mathrm {A}_n)))^2\notin \operatorname {cod}(G)$
, which is a contradiction.
Step 3:
![]() $\chi $
is faithful, for each nontrivial
$\chi $
is faithful, for each nontrivial
![]() $\chi \in \mathrm {Irr}(G|N):=\mathrm {Irr}(G)-\mathrm {Irr}(G/N$
).
$\chi \in \mathrm {Irr}(G|N):=\mathrm {Irr}(G)-\mathrm {Irr}(G/N$
).
From the proof of [Reference Dolorfino, Martin, Slonim, Sun and Yang8, Lemma 2.5],
By the definition of
![]() $\mathrm {Irr}(G|N)$
, it follows that if
$\mathrm {Irr}(G|N)$
, it follows that if
![]() $\chi \in \mathrm {Irr}(G|N),$
then
$\chi \in \mathrm {Irr}(G|N),$
then
![]() $N \not \leq \mathrm {ker}(\chi ).$
Thus, since N is the unique nontrivial, proper, normal subgroup of G,
$N \not \leq \mathrm {ker}(\chi ).$
Thus, since N is the unique nontrivial, proper, normal subgroup of G,
![]() $\mathrm {ker}(\chi ) = G$
or
$\mathrm {ker}(\chi ) = G$
or
![]() $\mathrm {ker}(\chi )~=~1$
. Therefore,
$\mathrm {ker}(\chi )~=~1$
. Therefore,
![]() $\mathrm {ker}(\chi ) = 1$
for all nontrivial
$\mathrm {ker}(\chi ) = 1$
for all nontrivial
![]() $\chi \in \mathrm {Irr}(G|N).$
$\chi \in \mathrm {Irr}(G|N).$
Step 4: N is an elementary abelian group.
Suppose that N is not abelian. Since N is a minimal normal subgroup, by [Reference Dixon and Mortimer7, Theorem 4.3A(iii)],
![]() $N=S^n$
, where S is a nonabelian simple group and
$N=S^n$
, where S is a nonabelian simple group and
![]() $n\in \mathbb {Z}^+$
. By [Reference Moretó14, Lemma 4.2] and [Reference James and Kerber11, Theorem 4.3.34], there is a nontrivial character
$n\in \mathbb {Z}^+$
. By [Reference Moretó14, Lemma 4.2] and [Reference James and Kerber11, Theorem 4.3.34], there is a nontrivial character
![]() $\chi \in \mathrm {Irr}(N)$
which extends to some
$\chi \in \mathrm {Irr}(N)$
which extends to some
![]() $\psi \in \mathrm {Irr}(G).$
Now, ker
$\psi \in \mathrm {Irr}(G).$
Now, ker
![]() $(\psi )=1$
by Step 3, so cod
$(\psi )=1$
by Step 3, so cod
![]() $(\psi )=|G|/\psi (1)=|G/N|\cdot |N|/\chi (1).$
However, by assumption,
$(\psi )=|G|/\psi (1)=|G/N|\cdot |N|/\chi (1).$
However, by assumption,
![]() $\mathrm {cod}(G)= \mathrm {cod}(\mathrm {A}_n)= \mathrm {cod}(G/N)$
. Thus, cod
$\mathrm {cod}(G)= \mathrm {cod}(\mathrm {A}_n)= \mathrm {cod}(G/N)$
. Thus, cod
![]() $(\psi ) \in \mathrm {cod}(G)= \mathrm {cod}(G/N),$
so
$(\psi ) \in \mathrm {cod}(G)= \mathrm {cod}(G/N),$
so
![]() $\mathrm {cod}(\psi )=|G/N|/\phi (1)$
for some
$\mathrm {cod}(\psi )=|G/N|/\phi (1)$
for some
![]() $\phi \in \mathrm {Irr}(G/N).$
Hence,
$\phi \in \mathrm {Irr}(G/N).$
Hence,
![]() $|G/N|$
is divisible by
$|G/N|$
is divisible by
![]() $\mathrm {cod}(\psi )$
which contradicts the fact that
$\mathrm {cod}(\psi )$
which contradicts the fact that
![]() $\mathrm {cod}(\psi )=|G/N|\cdot |N|/\chi (1),$
as
$\mathrm {cod}(\psi )=|G/N|\cdot |N|/\chi (1),$
as
![]() $\chi (1)\neq |N|.$
Thus, N must be abelian.
$\chi (1)\neq |N|.$
Thus, N must be abelian.
Now to show that N is elementary abelian, let a prime p divide
![]() $|N|.$
Then N has a p-Sylow subgroup K, and K is the unique p-Sylow subgroup of N since N is abelian, so K is characteristic in N. Thus, K is a normal subgroup of
$|N|.$
Then N has a p-Sylow subgroup K, and K is the unique p-Sylow subgroup of N since N is abelian, so K is characteristic in N. Thus, K is a normal subgroup of
![]() $G,$
so
$G,$
so
![]() $K=N$
as N is minimal. Thus,
$K=N$
as N is minimal. Thus,
![]() $|N|=p^n.$
Now, take the subgroup
$|N|=p^n.$
Now, take the subgroup
![]() $N^p=\{n^p \mid n \in N\}$
of
$N^p=\{n^p \mid n \in N\}$
of
![]() $N,$
which is proper by Cauchy’s theorem. Since
$N,$
which is proper by Cauchy’s theorem. Since
![]() $N^p$
is characteristic in
$N^p$
is characteristic in
![]() $N,$
it must be normal in
$N,$
it must be normal in
![]() $G,$
so
$G,$
so
![]() $N^p$
is trivial by the uniqueness of
$N^p$
is trivial by the uniqueness of
![]() $N.$
Thus, every element of N has order p and N is elementary abelian.
$N.$
Thus, every element of N has order p and N is elementary abelian.
Step 5:
![]() $\mathbf {C}_G(N) = N.$
$\mathbf {C}_G(N) = N.$
First note that since N is normal,
![]() $\mathbf {C}_G(N) \trianglelefteq G.$
Additionally, since N is abelian by Step 4,
$\mathbf {C}_G(N) \trianglelefteq G.$
Additionally, since N is abelian by Step 4,
![]() $N \leq \mathbf {C}_G(N)$
. By the maximality of
$N \leq \mathbf {C}_G(N)$
. By the maximality of
![]() $N,$
we must have
$N,$
we must have
![]() $\mathbf {C}_G(N) = N$
or
$\mathbf {C}_G(N) = N$
or
![]() $\mathbf {C}_G(N) = G.$
If
$\mathbf {C}_G(N) = G.$
If
![]() $\mathbf {C}_G(N) = N,$
we are done.
$\mathbf {C}_G(N) = N,$
we are done.
If not, then
![]() $\mathbf {C}_G(N) = G,$
so N must be in the centre of
$\mathbf {C}_G(N) = G,$
so N must be in the centre of
![]() $G.$
Then since N is the unique minimal normal subgroup of G by Step 2,
$G.$
Then since N is the unique minimal normal subgroup of G by Step 2,
![]() $|N|$
must be prime. If not, there always exists a proper nontrivial subgroup K of
$|N|$
must be prime. If not, there always exists a proper nontrivial subgroup K of
![]() $N,$
and K is normal since it is contained in
$N,$
and K is normal since it is contained in
![]() $\mathbf {Z}(G),$
contradicting the minimality of
$\mathbf {Z}(G),$
contradicting the minimality of
![]() $N.$
Hence, we have
$N.$
Hence, we have
![]() $N\le \mathbf {Z}(G)$
which implies that
$N\le \mathbf {Z}(G)$
which implies that
![]() $\mathbf {Z}(G)\cong N$
. This is because N is a maximal normal subgroup of G so if not, we would have
$\mathbf {Z}(G)\cong N$
. This is because N is a maximal normal subgroup of G so if not, we would have
![]() $\mathbf {Z}(G)=G$
, implying G is abelian which is a contradiction. Thus, N is isomorphic to a subgroup of the Schur multiplier of
$\mathbf {Z}(G)=G$
, implying G is abelian which is a contradiction. Thus, N is isomorphic to a subgroup of the Schur multiplier of
![]() $G/N$
by [Reference Isaacs10, Corollary 11.20].
$G/N$
by [Reference Isaacs10, Corollary 11.20].
Now, we note that it is well known that for
![]() $n>7$
, the Schur multiplier of
$n>7$
, the Schur multiplier of
![]() $\mathrm {A}_n$
is
$\mathrm {A}_n$
is
![]() $\mathbb {Z}_2,$
so
$\mathbb {Z}_2,$
so
![]() $G\cong 2.\mathrm {A}_n$
[Reference Wilson17]. From [Reference Bessenrodt and Olsson3, Theorem 4.3],
$G\cong 2.\mathrm {A}_n$
[Reference Wilson17]. From [Reference Bessenrodt and Olsson3, Theorem 4.3],
![]() $2.\mathrm {A}_n$
always has a faithful irreducible character
$2.\mathrm {A}_n$
always has a faithful irreducible character
![]() $\chi $
of degree
$\chi $
of degree
![]() $2^{\lfloor (n-2)/2\rfloor }$
. Recall that by Step 2, there is only one nontrivial proper normal subgroup of
$2^{\lfloor (n-2)/2\rfloor }$
. Recall that by Step 2, there is only one nontrivial proper normal subgroup of
![]() $G \cong 2.\mathrm {A}_n$
. In particular,
$G \cong 2.\mathrm {A}_n$
. In particular,
![]() $N \cong \mathbb {Z}_2$
is the only nontrivial proper normal subgroup of G. Thus,
$N \cong \mathbb {Z}_2$
is the only nontrivial proper normal subgroup of G. Thus,
![]() $|\mathrm {ker}(\chi )|~=~1$
or
$|\mathrm {ker}(\chi )|~=~1$
or
![]() $2$
. Then
$2$
. Then
![]() $\operatorname {cod}(\chi )={|2.\mathrm {A}_n:\mathrm {ker}(\chi )|}/{\chi (1)}$
. If
$\operatorname {cod}(\chi )={|2.\mathrm {A}_n:\mathrm {ker}(\chi )|}/{\chi (1)}$
. If
![]() $|\mathrm {ker}(\chi )|=1,$
then
$|\mathrm {ker}(\chi )|=1,$
then
![]() $\operatorname {cod}(\chi )={n!}/{2^{\lfloor (n-2)/2\rfloor }},$
and if
$\operatorname {cod}(\chi )={n!}/{2^{\lfloor (n-2)/2\rfloor }},$
and if
![]() $|\mathrm {ker}(\chi )|=2,$
then
$|\mathrm {ker}(\chi )|=2,$
then
![]() $\operatorname {cod}(\chi )={(n!/2)}/{2^{\lfloor (n-2)/2\rfloor }}= {n!}/{2^{\lfloor n/2\rfloor }}.$
In either case, for any prime
$\operatorname {cod}(\chi )={(n!/2)}/{2^{\lfloor (n-2)/2\rfloor }}= {n!}/{2^{\lfloor n/2\rfloor }}.$
In either case, for any prime
![]() $p\neq 2, |\operatorname {cod}(\chi )|_p=|n!|_p=|\mathrm {A}_n|_p$
. However,
$p\neq 2, |\operatorname {cod}(\chi )|_p=|n!|_p=|\mathrm {A}_n|_p$
. However,
![]() $\operatorname {cod}(\chi )\in \operatorname {cod}(\mathrm {A}_n)$
since
$\operatorname {cod}(\chi )\in \operatorname {cod}(\mathrm {A}_n)$
since
![]() $\operatorname {cod}(G)=\operatorname {cod}(\mathrm {A}_n)$
. Therefore, there is a character degree of
$\operatorname {cod}(G)=\operatorname {cod}(\mathrm {A}_n)$
. Therefore, there is a character degree of
![]() $\mathrm {A}_n$
which is a power of
$\mathrm {A}_n$
which is a power of
![]() $2$
.
$2$
.
However, from [Reference Malle and Zalesskii13], for
![]() $n>7, \mathrm {A}_n$
only has a character degree equal to a power of
$n>7, \mathrm {A}_n$
only has a character degree equal to a power of
![]() $2$
when
$2$
when
![]() $n=2^d+1$
for some positive integer d. In this case,
$n=2^d+1$
for some positive integer d. In this case,
![]() $2^d=n-1\in \mathrm {cd}(\mathrm {A}_n)$
so we need
$2^d=n-1\in \mathrm {cd}(\mathrm {A}_n)$
so we need
![]() ${|\mathrm {A}_n|}/{n-1}={|2.\mathrm {A}_n|}/{2^{\lfloor (n-2)/2\rfloor }}$
or
${|\mathrm {A}_n|}/{n-1}={|2.\mathrm {A}_n|}/{2^{\lfloor (n-2)/2\rfloor }}$
or
![]() ${|2.\mathrm {A}_n|}/{2^{\lfloor n/2\rfloor }}$
. Hence,
${|2.\mathrm {A}_n|}/{2^{\lfloor n/2\rfloor }}$
. Hence,
so
![]() $n-1=2^{\lfloor (n-2)/2\rfloor -1}$
or
$n-1=2^{\lfloor (n-2)/2\rfloor -1}$
or
![]() $2^{\lfloor n/2\rfloor -1}$
. However, the only integer solution to either of these equations occurs when
$2^{\lfloor n/2\rfloor -1}$
. However, the only integer solution to either of these equations occurs when
![]() $n=9$
and
$n=9$
and
![]() $9-1=8=2^3=2^{\lfloor 9/2\rfloor -1}$
. In this case, we check the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson6] to find that the codegree sets of
$9-1=8=2^3=2^{\lfloor 9/2\rfloor -1}$
. In this case, we check the ATLAS [Reference Conway, Curtis, Norton, Parker and Wilson6] to find that the codegree sets of
![]() $A_9$
and
$A_9$
and
![]() $2.A_9$
do not have the same order. This is a contradiction, so
$2.A_9$
do not have the same order. This is a contradiction, so
![]() $\mathbf {C}_G(N)=N$
.
$\mathbf {C}_G(N)=N$
.
Step 6. Let
![]() $\lambda $
be a nontrivial character in
$\lambda $
be a nontrivial character in
![]() $\mathrm {Irr}(N)$
and
$\mathrm {Irr}(N)$
and
![]() $\vartheta \in \mathrm {Irr}(I_G(\lambda )|\lambda ),$
the set of irreducible constituents of
$\vartheta \in \mathrm {Irr}(I_G(\lambda )|\lambda ),$
the set of irreducible constituents of
![]() $\lambda ^{I_G(\lambda )},$
where
$\lambda ^{I_G(\lambda )},$
where
![]() $I_G(\lambda )$
is the inertia group of
$I_G(\lambda )$
is the inertia group of
![]() $\lambda $
in G. Then
$\lambda $
in G. Then
![]() ${|I_G(\lambda )|}/{\vartheta (1)} \in \mathrm {cod}(G).$
Also,
${|I_G(\lambda )|}/{\vartheta (1)} \in \mathrm {cod}(G).$
Also,
![]() $\vartheta (1)$
divides
$\vartheta (1)$
divides
![]() $|I_G(\lambda )/N|$
and
$|I_G(\lambda )/N|$
and
![]() $|N|$
divides
$|N|$
divides
![]() $|G/N|.$
Lastly,
$|G/N|.$
Lastly,
![]() $I_G(\lambda ) < G,$
that is,
$I_G(\lambda ) < G,$
that is,
![]() $\lambda $
is not G-invariant.
$\lambda $
is not G-invariant.
Let
![]() $\lambda $
be a nontrivial character in
$\lambda $
be a nontrivial character in
![]() $\operatorname {Irr}(N)$
and
$\operatorname {Irr}(N)$
and
![]() $\vartheta \in \operatorname {Irr}(I_G(\lambda )|\lambda )$
. Let
$\vartheta \in \operatorname {Irr}(I_G(\lambda )|\lambda )$
. Let
![]() $\chi $
be an irreducible constituent of
$\chi $
be an irreducible constituent of
![]() $\vartheta ^G.$
By [Reference Isaacs10, Corollary 5.4],
$\vartheta ^G.$
By [Reference Isaacs10, Corollary 5.4],
![]() $\chi \in \operatorname {Irr}(G)$
, and by [Reference Isaacs10, Definition 5.1], we have
$\chi \in \operatorname {Irr}(G)$
, and by [Reference Isaacs10, Definition 5.1], we have
![]() $\chi (1) = ({|G|}/{|I_G(\lambda )|}) \cdot \vartheta (1)$
. Moreover,
$\chi (1) = ({|G|}/{|I_G(\lambda )|}) \cdot \vartheta (1)$
. Moreover,
![]() $\operatorname {ker}(\chi ) = 1$
by Step 2, and thus
$\operatorname {ker}(\chi ) = 1$
by Step 2, and thus
![]() $\operatorname {cod}(\chi ) = {|G|}/{\chi (1)} = {|I_G(\lambda )|}/{\vartheta (1)}$
, so
$\operatorname {cod}(\chi ) = {|G|}/{\chi (1)} = {|I_G(\lambda )|}/{\vartheta (1)}$
, so
![]() ${|I_G(\lambda )|}/{\vartheta (1)} \in \operatorname {cod}(G)$
. Now, since N is abelian,
${|I_G(\lambda )|}/{\vartheta (1)} \in \operatorname {cod}(G)$
. Now, since N is abelian,
![]() $\lambda (1) = 1$
, so we have
$\lambda (1) = 1$
, so we have
![]() $\vartheta (1) = \vartheta (1)/\lambda (1)$
which divides
$\vartheta (1) = \vartheta (1)/\lambda (1)$
which divides
![]() ${|I_G(\lambda )|}/{|N|}$
, so
${|I_G(\lambda )|}/{|N|}$
, so
![]() $|N|$
divides
$|N|$
divides
![]() ${|I_G(\lambda )|}/{\vartheta (1)}$
. Moreover,
${|I_G(\lambda )|}/{\vartheta (1)}$
. Moreover,
![]() $\operatorname {cod}(G) = \operatorname {cod}(G/N),$
and all elements in
$\operatorname {cod}(G) = \operatorname {cod}(G/N),$
and all elements in
![]() $\operatorname {cod}(G/N)$
divide
$\operatorname {cod}(G/N)$
divide
![]() $|G/N|$
, so
$|G/N|$
, so
![]() $|N|$
divides
$|N|$
divides
![]() $|G/N|$
.
$|G/N|$
.
Next, we want to show
![]() $I_G(\lambda )$
is a proper subgroup of G. To reach a contradiction, assume
$I_G(\lambda )$
is a proper subgroup of G. To reach a contradiction, assume
![]() $I_G(\lambda ) = G$
. Then
$I_G(\lambda ) = G$
. Then
![]() $\operatorname {ker}(\lambda ) \unlhd G$
. From Step 2,
$\operatorname {ker}(\lambda ) \unlhd G$
. From Step 2,
![]() $\operatorname {ker}(\lambda ) = 1,$
and from Step 4, N is a cyclic group of prime order. Thus, by the Normaliser–Centraliser theorem,
$\operatorname {ker}(\lambda ) = 1,$
and from Step 4, N is a cyclic group of prime order. Thus, by the Normaliser–Centraliser theorem,
![]() $G / N= \mathbf {N}_{G}(N) / \mathbf {C}_{G}(N) \leq \operatorname {Aut}(N)$
so
$G / N= \mathbf {N}_{G}(N) / \mathbf {C}_{G}(N) \leq \operatorname {Aut}(N)$
so
![]() $G / N$
is abelian, which is a contradiction.
$G / N$
is abelian, which is a contradiction.
Step 7: Final contradiction.
From Step 4, N is an elementary abelian group of order
![]() $p^m$
for some prime p and integer
$p^m$
for some prime p and integer
![]() $m\geq 1$
. By the Normaliser–Centraliser theorem,
$m\geq 1$
. By the Normaliser–Centraliser theorem,
![]() $\mathrm {A}_n \cong G/N = \mathbf {N}_G(N)/\mathbf {C}_G(N) \leq \mathrm {Aut}(N)$
and
$\mathrm {A}_n \cong G/N = \mathbf {N}_G(N)/\mathbf {C}_G(N) \leq \mathrm {Aut}(N)$
and
![]() $m>1$
. Note that in general,
$m>1$
. Note that in general,
![]() $\mathrm {Aut}(N)\cong \mathrm {GL}(m,p)$
. By Step 6,
$\mathrm {Aut}(N)\cong \mathrm {GL}(m,p)$
. By Step 6,
![]() $|N|$
divides
$|N|$
divides
![]() $|G/N|,$
so
$|G/N|,$
so
![]() $|N|=p^m$
divides
$|N|=p^m$
divides
![]() $|\mathrm {A}_n|$
and
$|\mathrm {A}_n|$
and
![]() $G/N\cong \mathrm {A}_n\lesssim \mathrm {GL}(m,p).$
We prove by contradiction that this cannot occur.
$G/N\cong \mathrm {A}_n\lesssim \mathrm {GL}(m,p).$
We prove by contradiction that this cannot occur.
First, we claim that if
![]() $p^m$
divides
$p^m$
divides
![]() $|\mathrm {A}_n|$
and
$|\mathrm {A}_n|$
and
![]() $\mathrm {A}_n\lesssim (\mathrm {GL}(m,p),$
then p must equal
$\mathrm {A}_n\lesssim (\mathrm {GL}(m,p),$
then p must equal
![]() $2$
. To show this, we note that for
$2$
. To show this, we note that for
![]() $p>2,$
by [Reference Bessenrodt, Tong-Viet and Zhang4], if
$p>2,$
by [Reference Bessenrodt, Tong-Viet and Zhang4], if
![]() $p^m$
divides
$p^m$
divides
![]() $|\mathrm {A}_n|,$
then
$|\mathrm {A}_n|,$
then
![]() $m < {n}/{2}$
. However, by [Reference Wagner16, Theorem 1.1], if
$m < {n}/{2}$
. However, by [Reference Wagner16, Theorem 1.1], if
![]() $n>6$
, the minimal faithful degree of a modular representation of
$n>6$
, the minimal faithful degree of a modular representation of
![]() $\mathrm {A}_n$
over a field of characteristic p is at least
$\mathrm {A}_n$
over a field of characteristic p is at least
![]() $n-2$
. Since embedding
$n-2$
. Since embedding
![]() $\mathrm {A}_n$
as a subgroup of
$\mathrm {A}_n$
as a subgroup of
![]() $\mathrm {GL}(m,p)$
is equivalent to giving a faithful representation of degree m over a field of characteristic p, we have
$\mathrm {GL}(m,p)$
is equivalent to giving a faithful representation of degree m over a field of characteristic p, we have
![]() $m\geq n-2$
. This is a contradiction since
$m\geq n-2$
. This is a contradiction since
![]() ${n}/{2}> n-2$
implies
${n}/{2}> n-2$
implies
![]() $n<4$
. Therefore,
$n<4$
. Therefore,
![]() $p=2$
.
$p=2$
.
Now, let
![]() $p=2$
. As above, from [Reference Bessenrodt, Tong-Viet and Zhang4], we obtain
$p=2$
. As above, from [Reference Bessenrodt, Tong-Viet and Zhang4], we obtain
![]() $|n!|_2\leq 2^{n-1}$
. Thus, if
$|n!|_2\leq 2^{n-1}$
. Thus, if
![]() $2^m$
divides
$2^m$
divides
![]() $|\mathrm {A}_n|,$
then
$|\mathrm {A}_n|,$
then
![]() $2^m \leq |\mathrm {A}_n|_2 \leq 2^{n-2}$
so
$2^m \leq |\mathrm {A}_n|_2 \leq 2^{n-2}$
so
![]() $m\le n-2.$
We will deal first with
$m\le n-2.$
We will deal first with
![]() $n>8$
and then treat the case
$n>8$
and then treat the case
![]() $n=8$
later. For
$n=8$
later. For
![]() $n>8$
, [Reference Wagner15, Theorem 1.1] shows that the minimal faithful degree of a modular representation of
$n>8$
, [Reference Wagner15, Theorem 1.1] shows that the minimal faithful degree of a modular representation of
![]() $\mathrm {A}_n$
over a field of characteristic
$\mathrm {A}_n$
over a field of characteristic
![]() $2$
is at least
$2$
is at least
![]() $n-2$
. Therefore, we must have
$n-2$
. Therefore, we must have
![]() $m\geq n-2$
, so we have equality,
$m\geq n-2$
, so we have equality,
![]() $m=n-2.$
$m=n-2.$
Let
![]() $\lambda \in \mathrm { Irr}(N), \vartheta \in \mathrm {Irr}(I_G(\lambda )|\lambda )$
and
$\lambda \in \mathrm { Irr}(N), \vartheta \in \mathrm {Irr}(I_G(\lambda )|\lambda )$
and
![]() $T := I_G(\lambda )$
. Then
$T := I_G(\lambda )$
. Then
![]() $1<|G:T|<|N|=2^{n-2}$
for
$1<|G:T|<|N|=2^{n-2}$
for
![]() $|G:T|$
is the number of all conjugates of
$|G:T|$
is the number of all conjugates of
![]() $\lambda $
. By Step 5,
$\lambda $
. By Step 5,
![]() ${|T|}/{\vartheta (1)}\in \mathrm {cod}(G)$
and moreover
${|T|}/{\vartheta (1)}\in \mathrm {cod}(G)$
and moreover
![]() $|N|$
divides
$|N|$
divides
![]() ${|T|}/{\vartheta (1)}$
. Since
${|T|}/{\vartheta (1)}$
. Since
![]() $|N|=|N|_2=|\mathrm {A}_n|_2$
and
$|N|=|N|_2=|\mathrm {A}_n|_2$
and
![]() $\mathrm {cod}(G)=\mathrm {cod}(\mathrm {A}_n)$
, it follows that
$\mathrm {cod}(G)=\mathrm {cod}(\mathrm {A}_n)$
, it follows that
![]() $|{|T|}/{\vartheta (1)}|_2=|N|.$
Thus,
$|{|T|}/{\vartheta (1)}|_2=|N|.$
Thus,
![]() $|{|T/N|}/{\vartheta (1)}|_2=1$
so the
$|{|T/N|}/{\vartheta (1)}|_2=1$
so the
![]() $2$
-parts of
$2$
-parts of
![]() $|T/N|$
and
$|T/N|$
and
![]() $\vartheta (1)$
are equal. Thus, for every
$\vartheta (1)$
are equal. Thus, for every
![]() $\vartheta \in \mathrm {Irr}(T\mid \lambda )$
, we have
$\vartheta \in \mathrm {Irr}(T\mid \lambda )$
, we have
![]() $|\vartheta (1)|_2=|T/N|_2.$
However,
$|\vartheta (1)|_2=|T/N|_2.$
However,
![]() $|T/N|= \sum _{\vartheta \in \mathrm {Irr}(T\mid \lambda )} \vartheta (1)^2.$
Hence, if
$|T/N|= \sum _{\vartheta \in \mathrm {Irr}(T\mid \lambda )} \vartheta (1)^2.$
Hence, if
![]() $|\vartheta (1)|_2=2^k\geq 2$
for every
$|\vartheta (1)|_2=2^k\geq 2$
for every
![]() $\vartheta \in \mathrm {Irr}(T\mid \lambda ),$
we would have
$\vartheta \in \mathrm {Irr}(T\mid \lambda ),$
we would have
![]() $|T/N|_2=2^{2k}$
, which contradicts the fact that
$|T/N|_2=2^{2k}$
, which contradicts the fact that
![]() $|\vartheta (1)|_2=|T/N|_2.$
Therefore,
$|\vartheta (1)|_2=|T/N|_2.$
Therefore,
![]() $|T/N|_2=1.$
Thus, since
$|T/N|_2=1.$
Thus, since
![]() $|G/N|_2\geq |N|=2^{n-2}$
, we have
$|G/N|_2\geq |N|=2^{n-2}$
, we have
![]() $|G:T|_2=|G/N:T/N|_2\geq 2^{n-2},$
so
$|G:T|_2=|G/N:T/N|_2\geq 2^{n-2},$
so
![]() $|G:T|\geq 2^{n-2}=|N|,$
which is a contradiction.
$|G:T|\geq 2^{n-2}=|N|,$
which is a contradiction.
Now we turn to the case
![]() $n=8$
. We have
$n=8$
. We have
![]() $p=2$
and
$p=2$
and
![]() $m=4,5$
or
$m=4,5$
or
![]() $6$
. In this case,
$6$
. In this case,
![]() $\mathrm {A}_8 \cong \mathrm {GL}(4,2)$
and
$\mathrm {A}_8 \cong \mathrm {GL}(4,2)$
and
![]() $2^6$
divides
$2^6$
divides
![]() $|\mathrm {A}_8|$
. We look at each possibility for m in turn. If
$|\mathrm {A}_8|$
. We look at each possibility for m in turn. If
![]() $m=6,$
then
$m=6,$
then
![]() $|N|_2=|\mathrm {A}_8|_2.$
For this case, the same argument as above holds since
$|N|_2=|\mathrm {A}_8|_2.$
For this case, the same argument as above holds since
![]() $6=8-2$
, and we reach a contradiction.
$6=8-2$
, and we reach a contradiction.
Second, let
![]() $m=5$
. As above,
$m=5$
. As above,
![]() $|G:T|<|N|=2^5$
and
$|G:T|<|N|=2^5$
and
![]() ${|T|}/{\vartheta (1)}\in \mathrm {cod}(G)$
such that
${|T|}/{\vartheta (1)}\in \mathrm {cod}(G)$
such that
![]() $2^5$
divides
$2^5$
divides
![]() ${|T|}/{\vartheta (1)}$
. Further,
${|T|}/{\vartheta (1)}$
. Further,
![]() $|{|T/N|}/{\vartheta (1)}|_2\leq 2$
so
$|{|T/N|}/{\vartheta (1)}|_2\leq 2$
so
![]() $|T/N|_2\leq 4$
and
$|T/N|_2\leq 4$
and
![]() $|G/N:T/N|_2\geq 16$
. Thus,
$|G/N:T/N|_2\geq 16$
. Thus,
![]() $16$
divides
$16$
divides
![]() $|G/N:T/N|$
and
$|G/N:T/N|$
and
![]() $|G/N:T/N|< 32.$
However, we may check the index of all subgroups of
$|G/N:T/N|< 32.$
However, we may check the index of all subgroups of
![]() $G/N\cong \text {A}_8$
using [Reference Conway, Curtis, Norton, Parker and Wilson6] and find that none of them satisfy these two properties.
$G/N\cong \text {A}_8$
using [Reference Conway, Curtis, Norton, Parker and Wilson6] and find that none of them satisfy these two properties.
Third, let
![]() $m=4$
. Then
$m=4$
. Then
![]() $G/N \cong \mathrm {A}_8 \cong \mathrm {GL}(4,2)$
and
$G/N \cong \mathrm {A}_8 \cong \mathrm {GL}(4,2)$
and
![]() $N=(\mathbb {Z}_2)^4$
so G is an extension of
$N=(\mathbb {Z}_2)^4$
so G is an extension of
![]() $\mathrm {GL}(4,2)$
by
$\mathrm {GL}(4,2)$
by
![]() $N.$
We may computationally calculate the codegree set for any such group using MAGMA [Reference Bosma and Playoust5]. There are only four such nonisomorphic extensions and we find that none of them have the same codegree set as
$N.$
We may computationally calculate the codegree set for any such group using MAGMA [Reference Bosma and Playoust5]. There are only four such nonisomorphic extensions and we find that none of them have the same codegree set as
![]() $\mathrm {A}_8$
. (The MAGMA code is available at https://github.com/zachslonim/Characterizing-Alternating-Groups-by-Their-Codegrees.) In every case,
$\mathrm {A}_8$
. (The MAGMA code is available at https://github.com/zachslonim/Characterizing-Alternating-Groups-by-Their-Codegrees.) In every case,
![]() $|N|=p^m$
produces a contradiction, so
$|N|=p^m$
produces a contradiction, so
![]() $N=1$
and
$N=1$
and
![]() $G\cong ~\mathrm {A}_n$
.
$G\cong ~\mathrm {A}_n$
.
Acknowledgements
The authors gratefully acknowledge the financial support of NSF and NSA, and also thank Texas State University for providing a great working environment and support. The authors would also like to thank Professor Richard Stanley for his help.