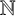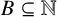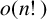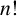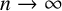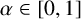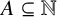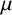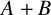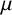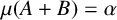1 Introduction
Let
![]() $\textsf {d}$
be the asymptotic (or natural) density on the nonnegative integers
$\textsf {d}$
be the asymptotic (or natural) density on the nonnegative integers
![]() $\mathbb N$
and
$\mathbb N$
and
![]() $\mathrm {dom}(\textsf {d})$
be the family of all sets
$\mathrm {dom}(\textsf {d})$
be the family of all sets
![]() $X \subseteq \mathbb {N}$
which possess asymptotic density, meaning that the limit of
$X \subseteq \mathbb {N}$
which possess asymptotic density, meaning that the limit of
![]() $| X \cap [1, n] |/n$
as
$| X \cap [1, n] |/n$
as
![]() $n \to \infty $
exists. We are going to show that, if
$n \to \infty $
exists. We are going to show that, if
![]() $B \subseteq \mathbb N$
is nonempty and ‘sufficiently small’, then there is a family of sets of the form
$B \subseteq \mathbb N$
is nonempty and ‘sufficiently small’, then there is a family of sets of the form
![]() $A+B$
with A and
$A+B$
with A and
![]() $A+B$
both in
$A+B$
both in
![]() $\mathrm {dom}(\textsf {d})$
such that the corresponding asymptotic densities attain every value in the interval
$\mathrm {dom}(\textsf {d})$
such that the corresponding asymptotic densities attain every value in the interval
![]() $[0,1]$
, where
$[0,1]$
, where
is the sumset of A and B (see Section 2 for details and examples). Writing
![]() $\mathbb {P}:=\{2,3,5,\ldots \}$
for the set of primes, we obtain as a special case the following result.
$\mathbb {P}:=\{2,3,5,\ldots \}$
for the set of primes, we obtain as a special case the following result.
Theorem 1.1. For each
![]() $\alpha \in [0,1]$
, there exists
$\alpha \in [0,1]$
, there exists
![]() $A \in \mathrm {dom}(\mathsf {d})$
such that
$A \in \mathrm {dom}(\mathsf {d})$
such that
![]() $A+\mathbb {P} \in \mathrm {dom}(\mathsf {d})$
and
$A+\mathbb {P} \in \mathrm {dom}(\mathsf {d})$
and
![]() $\mathsf {d}(A+\mathbb {P})=\alpha $
.
$\mathsf {d}(A+\mathbb {P})=\alpha $
.
In fact, our main result (Theorem 2.3) is much more general and stronger. It not only allows us to show that Theorem 1.1 holds with the primes replaced by a greater variety of sets and the asymptotic density
![]() $\textsf {d}$
replaced by any in a large class of axiomatically defined ‘densities’
$\textsf {d}$
replaced by any in a large class of axiomatically defined ‘densities’
![]() $\mu $
(including, among others, the Banach density, the analytic density and the logarithmic density), but it also does so uniformly in the choice of
$\mu $
(including, among others, the Banach density, the analytic density and the logarithmic density), but it also does so uniformly in the choice of
![]() $\mu $
.
$\mu $
.
The result, whose proof relies on the properties of a little known density first considered by Buck [Reference Buck2], belongs to a vast literature on the interplay between sumsets and their ‘largeness’ (see, for example, [Reference Bienvenu and Hennecart1, Reference Faisant, Grekos, Pandey and Somu5–Reference Hegyvári, Hennecart and Pach7, Reference Leonetti and Tringali11, Reference Volkmann13] and [Reference Ruzsa, Geroldinger and Ruzsa12, Sections 4 and 5]). Most notably, an analogue of Theorem 1.1 with
![]() $\mathbb {P}$
replaced by a nonempty finite set
$\mathbb {P}$
replaced by a nonempty finite set
![]() $B \subseteq \mathbb N$
(and without the additional requirement that
$B \subseteq \mathbb N$
(and without the additional requirement that
![]() $A \in \mathrm {dom}(\textsf {d})$
) was proved by Faisant et al. in [Reference Faisant, Grekos, Pandey and Somu5, Theorem 2.2]. A previous attempt to extend the latter to an infinite set B was made by Chu in [Reference Chu3, Theorem 1.5], but the proof turned out to be flawed [Reference Chu4]. So, Theorem 1.1 provides the first example in this direction (and is based on completely different ideas from [Reference Chu3, Reference Faisant, Grekos, Pandey and Somu5]).
$A \in \mathrm {dom}(\textsf {d})$
) was proved by Faisant et al. in [Reference Faisant, Grekos, Pandey and Somu5, Theorem 2.2]. A previous attempt to extend the latter to an infinite set B was made by Chu in [Reference Chu3, Theorem 1.5], but the proof turned out to be flawed [Reference Chu4]. So, Theorem 1.1 provides the first example in this direction (and is based on completely different ideas from [Reference Chu3, Reference Faisant, Grekos, Pandey and Somu5]).
1.1 Notation
We use
![]() $\mathbb Z$
for the integers and
$\mathbb Z$
for the integers and
![]() $\mathbb N^+$
for the positive integers. Given
$\mathbb N^+$
for the positive integers. Given
![]() $X \subseteq \mathbb {N}$
and
$X \subseteq \mathbb {N}$
and
![]() $q \in \mathbb {N}$
, we define
$q \in \mathbb {N}$
, we define
![]() $q \cdot \, X := \{qx \colon x \in X\}$
and
$q \cdot \, X := \{qx \colon x \in X\}$
and
![]() $X + q := X + \{q\}$
. We let an arithmetic progression (AP) be a set of the form
$X + q := X + \{q\}$
. We let an arithmetic progression (AP) be a set of the form
![]() $k\cdot \, \mathbb {N}+h$
with
$k\cdot \, \mathbb {N}+h$
with
![]() $k \in \mathbb N^+$
and
$k \in \mathbb N^+$
and
![]() $h \in \mathbb N$
, and we denote by
$h \in \mathbb N$
, and we denote by
![]() $\mathscr {A}$
the family of all finite unions of APs. Finally, for each
$\mathscr {A}$
the family of all finite unions of APs. Finally, for each
![]() $a, b \in \mathbb {Z}$
, we write
$a, b \in \mathbb {Z}$
, we write
![]() $[\![ a,b ]\!] := [a,b] \cap \mathbb {Z}$
for the discrete interval from a to b.
$[\![ a,b ]\!] := [a,b] \cap \mathbb {Z}$
for the discrete interval from a to b.
2 Preliminaries and main result
We say that a real-valued function
![]() $\mu ^{\star }$
defined on the power set
$\mu ^{\star }$
defined on the power set
![]() $\mathcal P(\mathbb N)$
of
$\mathcal P(\mathbb N)$
of
![]() $\mathbb N$
is an arithmetic upper density (on
$\mathbb N$
is an arithmetic upper density (on
![]() $\mathbb N$
) if, for all
$\mathbb N$
) if, for all
![]() $X, Y \subseteq \mathbb N$
, the following conditions are satisfied:
$X, Y \subseteq \mathbb N$
, the following conditions are satisfied:
-
(F1)
 $\mu ^{\star }(X) \le \mu ^{\star }(\mathbb N) = 1$
;
$\mu ^{\star }(X) \le \mu ^{\star }(\mathbb N) = 1$
; -
(F2)
 $\mu ^{\star }$
is monotone, that is, if
$\mu ^{\star }$
is monotone, that is, if
 $X \subseteq Y$
, then
$X \subseteq Y$
, then
 $\mu ^{\star }(X) \le \mu ^{\star }(Y)$
;
$\mu ^{\star }(X) \le \mu ^{\star }(Y)$
; -
(F3)
 $\mu ^{\star }$
is subadditive, that is,
$\mu ^{\star }$
is subadditive, that is,
 $\mu ^{\star }(X \cup Y) \le \mu ^{\star }(X) + \mu ^{\star }(Y)$
;
$\mu ^{\star }(X \cup Y) \le \mu ^{\star }(X) + \mu ^{\star }(Y)$
; -
(F4)
 $\mu ^{\star }(k \cdot \, X + h) = \mu ^{\star }(X)/k$
for every
$\mu ^{\star }(k \cdot \, X + h) = \mu ^{\star }(X)/k$
for every
 $k \in \mathbb N^+$
and
$k \in \mathbb N^+$
and
 $h \in \mathbb {N}$
.
$h \in \mathbb {N}$
.
Moreover, we call
![]() $\mu ^{\star }$
an arithmetic upper quasidensity (on
$\mu ^{\star }$
an arithmetic upper quasidensity (on
![]() $\mathbb N$
) if it satisfies (F1), (F3) and (F4).
$\mathbb N$
) if it satisfies (F1), (F3) and (F4).
Remark 2.1. While there do exist nonmonotone arithmetic upper quasidensities [Reference Leonetti and Tringali9, Theorem 1], such functions are not so interesting from the point of view of applications. Nevertheless, it seems meaningful to understand if monotonicity is critical to certain conclusions or can instead be dispensed with. This is our motivation for considering arithmetic upper quasidensities in spite of our main interest lying in the study of arithmetic upper densities (of course, the latter are a special case of the former).
We let the conjugate of an arithmetic upper quasidensity
![]() $\mu ^{\star }$
be the function
$\mu ^{\star }$
be the function
![]() $ \mu _{\star } \colon \mathcal {P}(\mathbb N) \to \mathbb R \colon X\mapsto 1-\mu ^{\star }(\mathbb N\setminus X)$
, and we refer to the restriction
$ \mu _{\star } \colon \mathcal {P}(\mathbb N) \to \mathbb R \colon X\mapsto 1-\mu ^{\star }(\mathbb N\setminus X)$
, and we refer to the restriction
![]() $\mu $
of
$\mu $
of
![]() $\mu ^{\star }$
to the set
$\mu ^{\star }$
to the set
as the arithmetic quasidensity induced by
![]() $\mu ^{\star }$
, or simply as an arithmetic quasidensity (on
$\mu ^{\star }$
, or simply as an arithmetic quasidensity (on
![]() $\mathbb N$
) if explicit reference to
$\mathbb N$
) if explicit reference to
![]() $\mu ^{\star }$
is unnecessary. Accordingly, we call
$\mu ^{\star }$
is unnecessary. Accordingly, we call
![]() $\mathcal D$
the domain of
$\mathcal D$
the domain of
![]() $\mu $
and denote it by
$\mu $
and denote it by
![]() $\text {dom}(\mu )$
.
$\text {dom}(\mu )$
.
Arithmetic upper (quasi)densities and arithmetic (quasi)densities were introduced in [Reference Leonetti and Tringali9] and further studied in [Reference Leonetti and Tringali8, Reference Leonetti and Tringali10, Reference Leonetti and Tringali11], though we are adding here the adjective ‘arithmetic’ to emphasise that they assign precise values to APs (see Proposition 3.1(iv) below).
Notable examples of arithmetic upper densities include the upper asymptotic, upper Banach, upper analytic, upper logarithmic, upper Pólya and upper Buck densities (see [Reference Leonetti and Tringali9, Section 6 and Examples 4, 5, 6 and 8]). In particular, we recall that the upper Buck density (on
![]() $\mathbb N$
) is the function
$\mathbb N$
) is the function
where
![]() $\textsf {d}^{\star }$
is the upper asymptotic density (on
$\textsf {d}^{\star }$
is the upper asymptotic density (on
![]() $\mathbb N$
), that is, the function
$\mathbb N$
), that is, the function
We will write
![]() $\mathfrak b_{\star }$
and
$\mathfrak b_{\star }$
and
![]() $\mathfrak b$
, respectively, for the conjugate of and the density induced by
$\mathfrak b$
, respectively, for the conjugate of and the density induced by
![]() $\mathfrak b^{\star }$
.
$\mathfrak b^{\star }$
.
Remark 2.2. The asymptotic density
![]() $\textsf {d}$
in Theorem 1.1 is just the density induced by
$\textsf {d}$
in Theorem 1.1 is just the density induced by
![]() $\textsf {d}^{\star }$
.
$\textsf {d}^{\star }$
.
We are ready to state the main theorem of the paper, whose proof we postpone to Section 3.
Theorem 2.3. Let
![]() $B\subseteq \mathbb {N}$
be a nonempty set such that
$B\subseteq \mathbb {N}$
be a nonempty set such that
![]() $\mathfrak {b}(B)=0$
. Then, for each
$\mathfrak {b}(B)=0$
. Then, for each
![]() $\alpha \in [0,1]$
, there exists
$\alpha \in [0,1]$
, there exists
![]() $A\subseteq \mathbb {N}$
such that
$A\subseteq \mathbb {N}$
such that
![]() $A \in \mathrm {dom}(\mu )$
and
$A \in \mathrm {dom}(\mu )$
and
![]() $\mu (A+B)=\alpha $
for all arithmetic quasidensities
$\mu (A+B)=\alpha $
for all arithmetic quasidensities
![]() $\mu $
.
$\mu $
.
Note that the analogous statement to Theorem 2.3 may not hold for a set B with a nonzero upper Buck density and a real number
![]() $\alpha \in [\mathfrak {b}^\star (B),1]$
. For example, if
$\alpha \in [\mathfrak {b}^\star (B),1]$
. For example, if
![]() $B \in \mathscr {A}$
, then the upper Buck density of
$B \in \mathscr {A}$
, then the upper Buck density of
![]() $A+B$
takes only a finite number of values as A varies over the subsets of
$A+B$
takes only a finite number of values as A varies over the subsets of
![]() $\mathbb N$
.
$\mathbb N$
.
The sets
![]() $B\subseteq \mathbb {N}$
such that
$B\subseteq \mathbb {N}$
such that
![]() $\mathfrak {b}(B)=0$
have been studied in [Reference Leonetti and Tringali10], where they are called small sets. Since
$\mathfrak {b}(B)=0$
have been studied in [Reference Leonetti and Tringali10], where they are called small sets. Since
![]() $\mathfrak {b}$
is monotone and subadditive, it is clear that the family of small sets is closed under finite unions and subsets. Examples of small sets include the finite sets, the factorials, the perfect powers and the primes. One may be tempted to conjecture that a set
$\mathfrak {b}$
is monotone and subadditive, it is clear that the family of small sets is closed under finite unions and subsets. Examples of small sets include the finite sets, the factorials, the perfect powers and the primes. One may be tempted to conjecture that a set
![]() $B\subseteq \mathbb {N}$
is small if (and only if) it is, in some sense, ‘sufficiently sparse’. However, the property of being small depends on the distribution of B through the APs of
$B\subseteq \mathbb {N}$
is small if (and only if) it is, in some sense, ‘sufficiently sparse’. However, the property of being small depends on the distribution of B through the APs of
![]() $\mathbb {N}$
(see Proposition 3.1(v)), so much so that the set
$\mathbb {N}$
(see Proposition 3.1(v)), so much so that the set
![]() $\{n!+n \colon n \in \mathbb {N}\}$
is not small (its upper Buck density is
$\{n!+n \colon n \in \mathbb {N}\}$
is not small (its upper Buck density is
![]() $1$
), in spite of being sparse, by any standards.
$1$
), in spite of being sparse, by any standards.
To date, it is not known whether nonmonotone arithmetic quasidensities exist (see Remark 2.1). However, arithmetic quasidensities satisfy a weak form of monotonicity (implicit in the proof of Proposition 3.1) that will be enough for our goals.
3 Proofs
To start with, we collect some basic properties of (upper and lower) quasidensities that will be used, possibly without further comment, in the proof of Theorem 2.3.
Proposition 3.1. Let
![]() $\mu _{\star }$
be the conjugate of an arithmetic upper quasidensity
$\mu _{\star }$
be the conjugate of an arithmetic upper quasidensity
![]() $\mu ^{\star }$
on
$\mu ^{\star }$
on
![]() $\mathbb N$
, and
$\mathbb N$
, and
![]() $\mu $
be the density induced by
$\mu $
be the density induced by
![]() $\mu ^{\star }$
. Then the following hold:
$\mu ^{\star }$
. Then the following hold:
-
(i)
 $\mathfrak b_{\star }(X) \le \mu _{\star }(X)\le \mu ^{\star }(X) \le \mathfrak b^{\star }(X)$
for every
$\mathfrak b_{\star }(X) \le \mu _{\star }(X)\le \mu ^{\star }(X) \le \mathfrak b^{\star }(X)$
for every
 $X\subseteq \mathbb N$
;
$X\subseteq \mathbb N$
; -
(ii) if
 $X \subseteq Y \subseteq \mathbb N$
, then
$X \subseteq Y \subseteq \mathbb N$
, then
 $\mathfrak b_{\star }(X) \le \mathfrak b_{\star }(Y)$
;
$\mathfrak b_{\star }(X) \le \mathfrak b_{\star }(Y)$
; -
(iii)
 $\mathscr {A}\subseteq \mathrm {dom}(\mathfrak {b}) \subseteq \mathrm {dom}(\mu )$
and
$\mathscr {A}\subseteq \mathrm {dom}(\mathfrak {b}) \subseteq \mathrm {dom}(\mu )$
and
 $\mu (X)=\mathfrak {b}(X)$
for every
$\mu (X)=\mathfrak {b}(X)$
for every
 $X \in \mathrm {dom}(\mathfrak b)$
;
$X \in \mathrm {dom}(\mathfrak b)$
; -
(iv) if
 $k \in \mathbb N^+$
and
$k \in \mathbb N^+$
and
 $H \subseteq [\![ 0, k-1 ]\!]$
, then
$H \subseteq [\![ 0, k-1 ]\!]$
, then
 $k \cdot \, \mathbb N + H \in \mathrm {dom}(\mathfrak b)$
and
$k \cdot \, \mathbb N + H \in \mathrm {dom}(\mathfrak b)$
and
 $\mathfrak b(k \cdot \, \mathbb N + H) = |H|/k$
;
$\mathfrak b(k \cdot \, \mathbb N + H) = |H|/k$
; -
(v)
 $\mathfrak {b}(X)=0$
if and only if X covers
$\mathfrak {b}(X)=0$
if and only if X covers
 $o(n!)$
residue classes modulo
$o(n!)$
residue classes modulo
 $n!$
as
$n!$
as
 $n\to \infty $
;
$n\to \infty $
; -
(vi) if
 $X \in \mathscr A$
, then
$X \in \mathscr A$
, then
 $X + Y \in \mathscr A$
for every
$X + Y \in \mathscr A$
for every
 $Y \subseteq \mathbb N$
.
$Y \subseteq \mathbb N$
.
Proof. See [Reference Leonetti and Tringali11, Proposition 2.1] for items (i)–(iv) and [Reference Leonetti and Tringali10, Proposition 2.6] for item (v). As for item (vi), let
![]() $X \in \mathscr {A}$
and
$X \in \mathscr {A}$
and
![]() $Y \subseteq \mathbb N$
. There then exist
$Y \subseteq \mathbb N$
. There then exist
![]() $k \in \mathbb {N}^+$
and
$k \in \mathbb {N}^+$
and
![]() $H\subseteq [\![ 0,k-1]\!]$
such that
$H\subseteq [\![ 0,k-1]\!]$
such that
![]() $X=k\cdot \, \mathbb {N}+H$
, and hence
$X=k\cdot \, \mathbb {N}+H$
, and hence
 $$ \begin{align*} X+Y=\bigcup_{y \in Y}(X+y)=\bigcup_{h \in H+Y}(k\cdot\, \mathbb{N}+h)=k\cdot\, \mathbb{N}+H', \end{align*} $$
$$ \begin{align*} X+Y=\bigcup_{y \in Y}(X+y)=\bigcup_{h \in H+Y}(k\cdot\, \mathbb{N}+h)=k\cdot\, \mathbb{N}+H', \end{align*} $$
where
![]() $H'$
is the finite set
$H'$
is the finite set
![]() $\bigcup _{i}\{\min ((H+Y)\cap (k\cdot \, \mathbb {N}+i)\}$
and the union is extended over all
$\bigcup _{i}\{\min ((H+Y)\cap (k\cdot \, \mathbb {N}+i)\}$
and the union is extended over all
![]() $i \in [\![ 0,k-1]\!]$
such that
$i \in [\![ 0,k-1]\!]$
such that
![]() $(H+Y)\cap (k\cdot \, \mathbb {N}+i) \ne \varnothing $
(with the understanding that an empty union is the empty set).
$(H+Y)\cap (k\cdot \, \mathbb {N}+i) \ne \varnothing $
(with the understanding that an empty union is the empty set).
We are ready for the proof of our main result. Note that the special case of a nonempty finite
![]() $B \subseteq \mathbb N$
was settled in [Reference Leonetti and Tringali11, Theorem 1.2] by a different argument.
$B \subseteq \mathbb N$
was settled in [Reference Leonetti and Tringali11, Theorem 1.2] by a different argument.
Proof of Theorem 2.3.
If
![]() $\alpha = 1$
, then the conclusion is obvious (by taking
$\alpha = 1$
, then the conclusion is obvious (by taking
![]() $A = \mathbb N$
). So, we assume from now on that
$A = \mathbb N$
). So, we assume from now on that
![]() $0 \le \alpha < 1$
. We divide the remainder of the proof into a series of three claims.
$0 \le \alpha < 1$
. We divide the remainder of the proof into a series of three claims.
Claim 1. There exist a sequence
![]() $(H_n)_{n \ge 1}$
of (nonempty) subsets of
$(H_n)_{n \ge 1}$
of (nonempty) subsets of
![]() $\mathbb N$
with
$\mathbb N$
with
![]() $H_n \subseteq [\![ 0, n! - 1 ]\!]$
and a sequence
$H_n \subseteq [\![ 0, n! - 1 ]\!]$
and a sequence
![]() $(h_n)_{n \ge 1}$
with
$(h_n)_{n \ge 1}$
with
![]() $h_n \in H_n$
such that, for all
$h_n \in H_n$
such that, for all
![]() $n \ge 1$
, the following hold:
$n \ge 1$
, the following hold:
-
(i)
 $\mathfrak b^{\star }(n! \cdot \, \mathbb N + H_n' + B) \le \alpha < \mathfrak b^{\star }(n! \cdot \, \mathbb N + H_n + B)$
, where
$\mathfrak b^{\star }(n! \cdot \, \mathbb N + H_n' + B) \le \alpha < \mathfrak b^{\star }(n! \cdot \, \mathbb N + H_n + B)$
, where
 $H_n' := H_n \setminus \{h_n\}$
;
$H_n' := H_n \setminus \{h_n\}$
; -
(ii)
 $n! \cdot \, \mathbb N + H_n' \subseteq H_{n+1} + (n+1)! \cdot \, \mathbb N \subseteq n! \cdot \, \mathbb N + H_n$
.
$n! \cdot \, \mathbb N + H_n' \subseteq H_{n+1} + (n+1)! \cdot \, \mathbb N \subseteq n! \cdot \, \mathbb N + H_n$
.
To prove Claim 1(i), we proceed by induction. The base case is clear by taking
![]() $H_1:=\{0\}$
and
$H_1:=\{0\}$
and
![]() $h_1:=0$
.
$h_1:=0$
.
As for the inductive step, fix
![]() $m \ge 1$
and suppose we have already found a set
$m \ge 1$
and suppose we have already found a set
![]() $H_m \subseteq [\![ 0, m! - 1 ]\!]$
and an integer
$H_m \subseteq [\![ 0, m! - 1 ]\!]$
and an integer
![]() $h_m \in H_m$
such that the claimed inequality holds for
$h_m \in H_m$
such that the claimed inequality holds for
![]() $n = m$
. Since
$n = m$
. Since
and
![]() $\mathfrak b^{\star }(m! \cdot \, \mathbb N + H_m' + B) \le \alpha < \mathfrak b^{\star }(m! \cdot \, \mathbb N + H_m + B)$
, there is a minimal
$\mathfrak b^{\star }(m! \cdot \, \mathbb N + H_m' + B) \le \alpha < \mathfrak b^{\star }(m! \cdot \, \mathbb N + H_m + B)$
, there is a minimal
![]() $k_{m+1} \in [\![ 0, m ]\!]$
such that
$k_{m+1} \in [\![ 0, m ]\!]$
such that
Consequently, we define
It is thus clear from (3.1) and the minimality of
![]() $k_{m+1}$
that the claimed inequality is also true for
$k_{m+1}$
that the claimed inequality is also true for
![]() $n = m+1$
. By induction, this is enough to complete the proof.
$n = m+1$
. By induction, this is enough to complete the proof.
(ii) This is now a straightforward consequence of the recursive construction of the sequences
![]() $(H_n)_{n \ge 1}$
and
$(H_n)_{n \ge 1}$
and
![]() $(h_n)_{n \ge 1}$
, as given in the inductive step of the proof of item (i). This proves our claim.
$(h_n)_{n \ge 1}$
, as given in the inductive step of the proof of item (i). This proves our claim.
Claim 2. Set
![]() $A := \bigcap _{n \ge 1} A_n$
, where
$A := \bigcap _{n \ge 1} A_n$
, where
![]() $A_n := n! \cdot \, \mathbb N + H_n$
. Then,
$A_n := n! \cdot \, \mathbb N + H_n$
. Then,
![]() $A \in \mathrm {dom}(\mathfrak b)$
.
$A \in \mathrm {dom}(\mathfrak b)$
.
To prove our claim, pick
![]() $n \in \mathbb N^+$
. It follows from Claim 1(ii) that
$n \in \mathbb N^+$
. It follows from Claim 1(ii) that
![]() $A_n\setminus (n!\cdot \, \mathbb {N}+h_n) \subseteq A \subseteq A_n$
. Considering that
$A_n\setminus (n!\cdot \, \mathbb {N}+h_n) \subseteq A \subseteq A_n$
. Considering that
![]() $A_n$
and
$A_n$
and
![]() $A_n\setminus (n!\cdot \, \mathbb {N}+h_n)$
are both in
$A_n\setminus (n!\cdot \, \mathbb {N}+h_n)$
are both in
![]() $\mathscr {A}$
, and
$\mathscr {A}$
, and
![]() $\mathscr A$
is contained in
$\mathscr A$
is contained in
![]() $\mathrm {dom}(\mathfrak b)$
, we obtain
$\mathrm {dom}(\mathfrak b)$
, we obtain
However, Claim 1(ii) gives
![]() $A_{n+1} \subseteq A_n$
. Since
$A_{n+1} \subseteq A_n$
. Since
![]() $\mathfrak b$
is monotone, it follows that
$\mathfrak b$
is monotone, it follows that
![]() $\mathfrak b(A_n)$
tends to a limit as
$\mathfrak b(A_n)$
tends to a limit as
![]() $n \to \infty $
. So, (3.2) implies that
$n \to \infty $
. So, (3.2) implies that
![]() $\mathfrak {b}_{\star }(A) = \mathfrak {b}^{\star }(A) = \lim _n \mathfrak b(A_n)$
and hence,
$\mathfrak {b}_{\star }(A) = \mathfrak {b}^{\star }(A) = \lim _n \mathfrak b(A_n)$
and hence,
![]() $A \in \mathrm {dom}(\mathfrak b)$
. This proves our claim.
$A \in \mathrm {dom}(\mathfrak b)$
. This proves our claim.
Claim 3.
![]() $A+B \in \mathrm {dom}(\mathfrak b)$
and
$A+B \in \mathrm {dom}(\mathfrak b)$
and
![]() $\mathfrak b(A+B) = \alpha $
.
$\mathfrak b(A+B) = \alpha $
.
To prove our claim, fix
![]() $n \in \mathbb N^+$
. We gather from Claim 1(ii) that
$n \in \mathbb N^+$
. We gather from Claim 1(ii) that
Considering that, by Proposition 3.1(vi),
![]() $X \in \mathscr {A}$
yields
$X \in \mathscr {A}$
yields
![]() $X+B \in \mathscr {A}$
and
$X+B \in \mathscr {A}$
and
![]() $\mathscr {A}\subseteq \mathrm {dom}(\mathfrak {b})$
, it follows that
$\mathscr {A}\subseteq \mathrm {dom}(\mathfrak {b})$
, it follows that
Now, fix
![]() $\varepsilon> 0$
. Since
$\varepsilon> 0$
. Since
![]() $\mathfrak {b}(B)=0$
, there exists
$\mathfrak {b}(B)=0$
, there exists
![]() $n_\varepsilon \in \mathbb N^+$
such that B covers at most
$n_\varepsilon \in \mathbb N^+$
such that B covers at most
![]() $\varepsilon \cdot \, n!$
residue classes modulo
$\varepsilon \cdot \, n!$
residue classes modulo
![]() $n!$
for all
$n!$
for all
![]() $n\ge n_\varepsilon $
. Consequently, we obtain from the subadditivity of
$n\ge n_\varepsilon $
. Consequently, we obtain from the subadditivity of
![]() $\mathfrak b^{\star }$
and Claim 1(i) that
$\mathfrak b^{\star }$
and Claim 1(i) that
However, the first inequality in the last display and Claim 1(i) imply
Therefore, (2) and (3) imply that
![]() $\alpha - \varepsilon < \mathfrak b_{\star }(A + B) \le \mathfrak b^{\star }(A + B) \le \alpha + \varepsilon $
for every
$\alpha - \varepsilon < \mathfrak b_{\star }(A + B) \le \mathfrak b^{\star }(A + B) \le \alpha + \varepsilon $
for every
![]() $\varepsilon> 0$
, which suffices to conclude that
$\varepsilon> 0$
, which suffices to conclude that
![]() $A+B \in \mathrm {dom}(\mathfrak b)$
and
$A+B \in \mathrm {dom}(\mathfrak b)$
and
![]() $\mathfrak b(A + B) = \alpha $
. This proves our claim.
$\mathfrak b(A + B) = \alpha $
. This proves our claim.
By Proposition 3.1(iii) and Claims 2 and 3, this is enough to finish the proof of the theorem.
Proof of Theorem 1.1.
This is now straightforward from Theorem 2.3 and Remark 2.2, when considering that the Buck density of the set of primes is zero (as already noted in Section 2).
As a final remark, we point out that, mutatis mutandis, all the results of this paper carry over to arithmetic (upper) quasidensities on
![]() $\mathbb Z$
, in the same spirit of [Reference Leonetti and Tringali8–Reference Leonetti and Tringali11].
$\mathbb Z$
, in the same spirit of [Reference Leonetti and Tringali8–Reference Leonetti and Tringali11].
Acknowledgment
We are grateful to an anonymous referee for his careful reading of the paper.