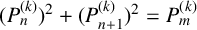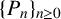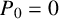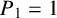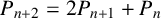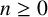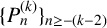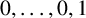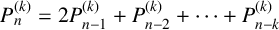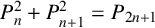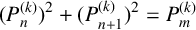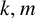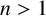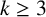1 Introduction
The Pell sequence
![]() ${\{P_n\}_{n\ge 0}}$
is the second-order linear recurrence defined by
${\{P_n\}_{n\ge 0}}$
is the second-order linear recurrence defined by
![]() ${P_{n+2}=2P_{n+1}+P_n}$
with initial conditions
${P_{n+2}=2P_{n+1}+P_n}$
with initial conditions
![]() $P_0=0$
and
$P_0=0$
and
![]() $P_1=1$
. A few terms of this sequence are
$P_1=1$
. A few terms of this sequence are
Diophantine equations related to the sums of powers of consecutive Pell numbers were studied by several authors. For example, motivated by the well-known identity
which tells us that the sum of the squares of two consecutive Pell numbers is still a Pell number, Rihane et al. [Reference Rihane, Luca, Faye and Togbe6] studied the Diophantine equation
and gave all the solutions of this equation in nonnegative integers
![]() $m, n$
and x. Ddamulira and Luca [Reference Ddamulira and Luca2] considered the more general Diophantine equation
$m, n$
and x. Ddamulira and Luca [Reference Ddamulira and Luca2] considered the more general Diophantine equation
in nonnegative integers
![]() $(n,m,x)$
, where
$(n,m,x)$
, where
![]() $\boldsymbol {U}=(U_n)_{n\ge 0}$
is the Lucas sequence given by
$\boldsymbol {U}=(U_n)_{n\ge 0}$
is the Lucas sequence given by
![]() $U_0=0$
,
$U_0=0$
,
![]() $U_1=1$
and
$U_1=1$
and
![]() $U_{n+2}=rU_{n+1}+U_n$
for all
$U_{n+2}=rU_{n+1}+U_n$
for all
![]() $n\ge 0$
. (Note that
$n\ge 0$
. (Note that
![]() $\boldsymbol {U}$
coincides with the Pell sequence when
$\boldsymbol {U}$
coincides with the Pell sequence when
![]() $r=2$
.)
$r=2$
.)
Luca et al. [Reference Luca, Tchammou and Togbé5] found all the solutions of the Diophantine equation
in positive integers
![]() $(m,n,k,x)$
and Faye et al. [Reference Faye, Gómez, Rihane, Luca and Togbé3] considered the more general exponential Diophantine equation
$(m,n,k,x)$
and Faye et al. [Reference Faye, Gómez, Rihane, Luca and Togbé3] considered the more general exponential Diophantine equation
in positive integers
![]() $(m,n,x,y)$
.
$(m,n,x,y)$
.
For an integer
![]() $k\ge 2$
, we consider a generalisation of the Pell sequence called the k-generalised Pell sequence or, for simplicity, the k-Pell sequence
$k\ge 2$
, we consider a generalisation of the Pell sequence called the k-generalised Pell sequence or, for simplicity, the k-Pell sequence
![]() $P^{(k)}=\{P^{(k)}_n\}_{n\ge -(k-2)}$
given by the higher order linear recurrence,
$P^{(k)}=\{P^{(k)}_n\}_{n\ge -(k-2)}$
given by the higher order linear recurrence,
with the initial conditions
![]() $P^{(k)}_{-(k-2)}=P^{(k)}_{-(k-3)}=\cdots =P^{(k)}_0=0$
and
$P^{(k)}_{-(k-2)}=P^{(k)}_{-(k-3)}=\cdots =P^{(k)}_0=0$
and
![]() $P^{(k)}_1=1$
. Note that this generalisation is in fact a family of sequences, where each new choice of k generates a distinct sequence. In particular, the usual Pell sequence is obtained for
$P^{(k)}_1=1$
. Note that this generalisation is in fact a family of sequences, where each new choice of k generates a distinct sequence. In particular, the usual Pell sequence is obtained for
![]() $k=2$
, that is,
$k=2$
, that is,
![]() $P^{(2)}_n=P_n$
.
$P^{(2)}_n=P_n$
.
Motivated by the above results, we look at the identity (1.1) in k-generalised Pell numbers. More precisely, we prove the following theorem.
Theorem 1.1. The Diophantine equation
has no positive integer solutions
![]() $(n,k,m)$
with
$(n,k,m)$
with
![]() $n>1$
and
$n>1$
and
![]() $k\ge 3$
.
$k\ge 3$
.
Usually, such a type of Diophantine equations require Baker-type estimates for lower bounds for linear forms in the logarithms of algebraic numbers as well as reduction techniques involving the theory of continued fractions (the Baker–Davenport method and the LLL algorithm). In our case, we will use only elementary properties of k-Pell numbers.
2 Auxiliary results
In this section, we shall collect some facts and tools which will be used later.
The characteristic polynomial of
![]() $P^{(k)}$
is
$P^{(k)}$
is
and it is irreducible over
![]() $\mathbb {Q}[x]$
with just one root
$\mathbb {Q}[x]$
with just one root
![]() $\gamma :=\gamma (k)$
outside the unit circle. The other roots are strictly inside the unit circle, that is,
$\gamma :=\gamma (k)$
outside the unit circle. The other roots are strictly inside the unit circle, that is,
![]() $\gamma $
is a Pisot number of degree k. This positive real root is called the dominant root of
$\gamma $
is a Pisot number of degree k. This positive real root is called the dominant root of
![]() $\Phi _k(x)$
.
$\Phi _k(x)$
.
In [Reference Bravo, Herrera and Luca1], the Binet-like formula for the k-Pell numbers is given by
 $$ \begin{align} P^{(k)}_n=\sum_{i=1}^k\frac{\gamma_i-1}{(k+1)\gamma^2_i-3k\gamma_i+k-1}\gamma^n_i, \end{align} $$
$$ \begin{align} P^{(k)}_n=\sum_{i=1}^k\frac{\gamma_i-1}{(k+1)\gamma^2_i-3k\gamma_i+k-1}\gamma^n_i, \end{align} $$
where
![]() $\gamma =\gamma _1,\ldots ,\gamma _k$
are the roots of the characteristic polynomial
$\gamma =\gamma _1,\ldots ,\gamma _k$
are the roots of the characteristic polynomial
![]() $\Phi _k(x)$
. The contribution of the roots inside the unit circle in (2.1) is almost trivial. More precisely, it was proved that the approximation
$\Phi _k(x)$
. The contribution of the roots inside the unit circle in (2.1) is almost trivial. More precisely, it was proved that the approximation
holds for all
![]() $n\ge 2-k$
, where
$n\ge 2-k$
, where
From (2.2), we can write
Also, we have the inequality
Furthermore, Kılıç and Taşci [Reference Kılıç and Taşci4] showed that the terms of the k-Pell sequence with indices
![]() $n\in \{1,2,\ldots ,k+1\}$
coincide with the first
$n\in \{1,2,\ldots ,k+1\}$
coincide with the first
![]() $k+1$
terms of the Fibonacci sequence with positive odd indices, that is,
$k+1$
terms of the Fibonacci sequence with positive odd indices, that is,
In the next lemma, we gather some technical results that will be used later.
Lemma 2.1 [Reference Bravo, Herrera and Luca1, Lemma 3.2].
Let
![]() $k,l\ge 2$
be integers.
$k,l\ge 2$
be integers.
-
(a) If
 $k>l$
, then
$k>l$
, then
 $\gamma (k)>\gamma (l)$
.
$\gamma (k)>\gamma (l)$
. -
(b)
 $\phi ^2(1-\phi ^{-k})<\gamma (k)<\phi ^2$
, where
$\phi ^2(1-\phi ^{-k})<\gamma (k)<\phi ^2$
, where
 $\phi =\tfrac 12(1+\sqrt {5})$
is the golden section.
$\phi =\tfrac 12(1+\sqrt {5})$
is the golden section. -
(c) If
 $k\ge 6$
, then
$k\ge 6$
, then
 $\phi ^2-k^{-1}<\phi ^2(1-\phi ^{-k})<\gamma (k)<\phi ^2$
.
$\phi ^2-k^{-1}<\phi ^2(1-\phi ^{-k})<\gamma (k)<\phi ^2$
. -
(d)
 $g_k(x)$
defined in (2.3) as a function of a real variable is positive, continuous and decreasing in the interval
$g_k(x)$
defined in (2.3) as a function of a real variable is positive, continuous and decreasing in the interval
 $(c_k,\infty )$
, where
$(c_k,\infty )$
, where
 $c_k={(3k+\sqrt {5k^2+4})}/{2(k+1)}$
. Moreover,
$c_k={(3k+\sqrt {5k^2+4})}/{2(k+1)}$
. Moreover,
 $g_k(\phi ^2)={1}/{(\phi +2)}$
.
$g_k(\phi ^2)={1}/{(\phi +2)}$
. -
(e)
 $0.276<g_k(\gamma (k))<0.5$
.
$0.276<g_k(\gamma (k))<0.5$
.
Note that for
![]() $k\ge 10$
, the value of
$k\ge 10$
, the value of
![]() $g_k(\gamma )$
is not greater than
$g_k(\gamma )$
is not greater than
![]() $0.31$
, as can be seen from
$0.31$
, as can be seen from
![]() $g_k(\gamma )<g_k(\phi ^2(1-\phi ^{-k}))$
.
$g_k(\gamma )<g_k(\phi ^2(1-\phi ^{-k}))$
.
We will also require a lemma that lists all cases when the sum of squares of any two Fibonacci numbers becomes a Fibonacci number.
Lemma 2.2 [Reference Şiar7, Theorem 1.1].
Let
![]() $n, m, r$
be positive integers such that
$n, m, r$
be positive integers such that
![]() $m\le n$
and let
$m\le n$
and let
![]() $(n,m,r)$
be a solution of the Diophantine equation
$(n,m,r)$
be a solution of the Diophantine equation
![]() $F^2_n+F^2_m=F_r$
. Then
$F^2_n+F^2_m=F_r$
. Then
3 Proof
Proof of Theorem 1.1.
When
![]() $n=2$
, one has
$n=2$
, one has
![]() $(P^{(k)}_2)^2+(P^{(k)}_3)^2 =2^2+ 5^2=29$
; however,
$(P^{(k)}_2)^2+(P^{(k)}_3)^2 =2^2+ 5^2=29$
; however,
![]() $P^{(k)}_m$
belongs to the increasing sequence
$P^{(k)}_m$
belongs to the increasing sequence
![]() $13,33,34,84, 88,\ldots $
for
$13,33,34,84, 88,\ldots $
for
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $m\ge 4$
. Thus, there is no solution for
$m\ge 4$
. Thus, there is no solution for
![]() $n=2$
. So we may suppose that
$n=2$
. So we may suppose that
![]() $n\ge 3$
.
$n\ge 3$
.
From the estimates in (2.4), we obtain
and
where we used
![]() $1+{1}/{\gamma ^2(k)}<1+{1}/{\gamma ^2(3)}<2<\gamma (k)$
. Thus, if
$1+{1}/{\gamma ^2(k)}<1+{1}/{\gamma ^2(3)}<2<\gamma (k)$
. Thus, if
![]() $(m,n,k)$
is a solution of (1.2), then
$(m,n,k)$
is a solution of (1.2), then
![]() $m\in \{2n,2n+1,2n+2\}$
.
$m\in \{2n,2n+1,2n+2\}$
.
Next, if
![]() $3\le n\le 5$
and
$3\le n\le 5$
and
![]() $3\le k\le 12$
, then finite computations in Mathematica yield no solutions for (1.2), whereas if
$3\le k\le 12$
, then finite computations in Mathematica yield no solutions for (1.2), whereas if
![]() $3\le n\le 5$
and
$3\le n\le 5$
and
![]() $k>12$
, then all three numbers
$k>12$
, then all three numbers
![]() $P^{(k)}_n$
,
$P^{(k)}_n$
,
![]() $P^{(k)}_{n+1}$
and
$P^{(k)}_{n+1}$
and
![]() $P^{(k)}_m$
are Fibonacci numbers with odd indices:
$P^{(k)}_m$
are Fibonacci numbers with odd indices:
By Lemma 2.2, the sum of the first two squares cannot be the third value. So, from now on,
![]() $n>5$
independently of k.
$n>5$
independently of k.
Let
![]() $m=2k+i$
,
$m=2k+i$
,
![]() $i\in \{0,1,2\}$
. Then (1.2) can be written as
$i\in \{0,1,2\}$
. Then (1.2) can be written as
Divide both sides by
![]() $\gamma ^{2n}$
to get
$\gamma ^{2n}$
to get
We write
where
Similarly,
where
 $$ \begin{align} |\mathscr{C}_2| & =|2g_k(\gamma)\gamma\mathscr{E}_k(n+1)/\gamma^n+(\mathscr{E}_k(n+1)/\gamma^n)^2| \notag \\ &\le2\cdot(1/2)\cdot3\cdot(1/2)\cdot\gamma^{-n}+(1/4)\cdot\gamma^{-2n}<2\gamma^{-n}. \end{align} $$
$$ \begin{align} |\mathscr{C}_2| & =|2g_k(\gamma)\gamma\mathscr{E}_k(n+1)/\gamma^n+(\mathscr{E}_k(n+1)/\gamma^n)^2| \notag \\ &\le2\cdot(1/2)\cdot3\cdot(1/2)\cdot\gamma^{-n}+(1/4)\cdot\gamma^{-2n}<2\gamma^{-n}. \end{align} $$
Since
![]() $|\mathscr {C}_3|=|\mathscr {E}_k(2n+i)/\gamma ^{2n}|<\gamma ^{-n}$
, we obtain from (3.1), (3.2) and (3.3) that
$|\mathscr {C}_3|=|\mathscr {E}_k(2n+i)/\gamma ^{2n}|<\gamma ^{-n}$
, we obtain from (3.1), (3.2) and (3.3) that
 $$ \begin{align} |g_k(\gamma)+g_k(\gamma)\gamma^2-\gamma^i|=\frac{1}{g}|\mathscr{C}_3-\mathscr{C}_1-\mathscr{C}_2|<4\cdot\bigg(\frac{1}{\gamma^n}+\frac{2}{\gamma^n}+\frac{1}{\gamma^n}\bigg)=\frac{16}{\gamma^n}. \end{align} $$
$$ \begin{align} |g_k(\gamma)+g_k(\gamma)\gamma^2-\gamma^i|=\frac{1}{g}|\mathscr{C}_3-\mathscr{C}_1-\mathscr{C}_2|<4\cdot\bigg(\frac{1}{\gamma^n}+\frac{2}{\gamma^n}+\frac{1}{\gamma^n}\bigg)=\frac{16}{\gamma^n}. \end{align} $$
Computing the left-hand side of (3.4) for
![]() $k=3,4,\ldots ,9$
and
$k=3,4,\ldots ,9$
and
![]() $i\in \{0,1,2\}$
, we obtain
$i\in \{0,1,2\}$
, we obtain
 $$ \begin{align*} 0.241<|g_k(\gamma)+g_k(\gamma)\gamma^2-\gamma^i|<\frac{16}{\gamma^n}<\frac{16}{2.54^n}, \end{align*} $$
$$ \begin{align*} 0.241<|g_k(\gamma)+g_k(\gamma)\gamma^2-\gamma^i|<\frac{16}{\gamma^n}<\frac{16}{2.54^n}, \end{align*} $$
which contradicts the fact that
![]() $n>5$
.
$n>5$
.
Now, suppose
![]() $k\ge 10$
. If
$k\ge 10$
. If
![]() $i=0$
, then in the left-hand side of (3.4),
$i=0$
, then in the left-hand side of (3.4),
 $$ \begin{align*} g_k(\gamma)\gamma^2+g_k(\gamma)-1>\frac{(\phi^2(1-\phi^{-10}))^2}{\phi+2}+\frac{1}{\phi+2}-1>1.14, \end{align*} $$
$$ \begin{align*} g_k(\gamma)\gamma^2+g_k(\gamma)-1>\frac{(\phi^2(1-\phi^{-10}))^2}{\phi+2}+\frac{1}{\phi+2}-1>1.14, \end{align*} $$
leading to
![]() $2.54^n<14.04$
, which is false for
$2.54^n<14.04$
, which is false for
![]() $n>5$
. So,
$n>5$
. So,
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
If
![]() $i=1$
, then
$i=1$
, then
and
![]() $g_k(\gamma )<0.31$
, so
$g_k(\gamma )<0.31$
, so
![]() $\gamma -g_k(\gamma )\gamma ^2-g_k(\gamma )>2.59-0.31\phi ^4-0.31>0.15$
and we get
$\gamma -g_k(\gamma )\gamma ^2-g_k(\gamma )>2.59-0.31\phi ^4-0.31>0.15$
and we get
![]() $\gamma ^n<106.7$
, which is false for
$\gamma ^n<106.7$
, which is false for
![]() $\gamma>2.59$
and
$\gamma>2.59$
and
![]() $n>5$
.
$n>5$
.
Similarly, if
![]() $i=2$
, we also have
$i=2$
, we also have
![]() $g_k(\gamma )<0.31$
and
$g_k(\gamma )<0.31$
and
![]() $\gamma>2.59$
. It follows that
$\gamma>2.59$
. It follows that
![]() $\gamma ^2-g_k(\gamma )\gamma ^2-g_k(\gamma )>2.59^2-0.31\phi ^4-0.31>4.27$
, which is even larger than the previous estimate, giving us again a contradiction. This completes the proof.
$\gamma ^2-g_k(\gamma )\gamma ^2-g_k(\gamma )>2.59^2-0.31\phi ^4-0.31>4.27$
, which is even larger than the previous estimate, giving us again a contradiction. This completes the proof.
Acknowledgement
The author would like to thank the anonymous referee for useful comments.