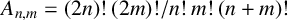1 Introduction
The Catalan numbers, given by
 $$ \begin{align*} C_n=\frac{1}{n+1}{2n\choose n},\quad n\ge 0, \end{align*} $$
$$ \begin{align*} C_n=\frac{1}{n+1}{2n\choose n},\quad n\ge 0, \end{align*} $$
occur in various counting problems. For instance,
![]() $C_n$
is the number of monotonic lattice paths along the edges of a grid with
$C_n$
is the number of monotonic lattice paths along the edges of a grid with
![]() $n\times n$
square cells, which do not pass above the diagonal, and is also the number of permutations of
$n\times n$
square cells, which do not pass above the diagonal, and is also the number of permutations of
![]() $\{1,\ldots ,n\}$
that avoid the permutation pattern
$\{1,\ldots ,n\}$
that avoid the permutation pattern
![]() $123$
, that is, with no three-term increasing subsequence. We refer to [Reference Stanley12] for many different combinatorial interpretations of the Catalan numbers.
$123$
, that is, with no three-term increasing subsequence. We refer to [Reference Stanley12] for many different combinatorial interpretations of the Catalan numbers.
Although the Catalan numbers naturally arise in combinatorics, they also possess rich arithmetic properties. One of the remarkable examples is the following congruence due to Sun and Tauraso [Reference Sun and Tauraso13]:
 $$ \begin{align} &\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\bigg(\frac{p}{3}\bigg)- \frac{1}{2}\pmod{p^2}. \end{align} $$
$$ \begin{align} &\sum_{k=0}^{p-1}C_k\equiv\frac{3}{2}\bigg(\frac{p}{3}\bigg)- \frac{1}{2}\pmod{p^2}. \end{align} $$
Here and in what follows,
![]() $p\ge 5$
is a prime and
$p\ge 5$
is a prime and
![]() $(\frac{\cdot}{\cdot })$
denotes the Legendre symbol. We remark that Tauraso [Reference Tauraso14, Theorem 6.1] established an interesting q-analogue of the modulo p version of (1.1), which was further generalised to a q-analogue of the modulo
$(\frac{\cdot}{\cdot })$
denotes the Legendre symbol. We remark that Tauraso [Reference Tauraso14, Theorem 6.1] established an interesting q-analogue of the modulo p version of (1.1), which was further generalised to a q-analogue of the modulo
![]() $p^2$
version by the first author [Reference Liu9, Theorem 1].
$p^2$
version by the first author [Reference Liu9, Theorem 1].
In 1874, Catalan [Reference Catalan3] observed that the numbers
![]() $A_{n,m}={(2n)!(2m)!}/{n!m!(n+m)!}$
are always integral. Since
$A_{n,m}={(2n)!(2m)!}/{n!m!(n+m)!}$
are always integral. Since
![]() $A_{n,1}/2$
coincides with the Catalan number
$A_{n,1}/2$
coincides with the Catalan number
![]() $C_n$
, these
$C_n$
, these
![]() $A_{n,m}$
were named the super Catalan numbers by Gessel [Reference Gessel6]. The integrality of
$A_{n,m}$
were named the super Catalan numbers by Gessel [Reference Gessel6]. The integrality of
![]() $A_{n,m}$
can also be deduced from Von Szily’s identity [Reference Von Szily15]:
$A_{n,m}$
can also be deduced from Von Szily’s identity [Reference Von Szily15]:
 $$ \begin{align} A_{n,m}=\sum_{k=-\infty}^{\infty}(-1)^k{2n\choose n+k}{2m\choose m+k}. \end{align} $$
$$ \begin{align} A_{n,m}=\sum_{k=-\infty}^{\infty}(-1)^k{2n\choose n+k}{2m\choose m+k}. \end{align} $$
There are interpretations of
![]() $A_{n,m}$
for some special values of m (see, for example, [Reference Allen and Gheorghiciuc1, Reference Chen and Wang4, Reference Pippenger and Schleich11]). However, it is still an open problem to find a general combinatorial interpretation for the super Catalan numbers.
$A_{n,m}$
for some special values of m (see, for example, [Reference Allen and Gheorghiciuc1, Reference Chen and Wang4, Reference Pippenger and Schleich11]). However, it is still an open problem to find a general combinatorial interpretation for the super Catalan numbers.
In 2018, Apagodu [Reference Apagodu2, Conjecture 2] proposed two conjectural congruences on double sums of super Catalan numbers, one of which is
 $$ \begin{align} \sum_{i=0}^{p-1}\sum_{j=0}^{p-1}A_{i,j}\equiv \bigg(\frac{p}{3}\bigg)\pmod{p}. \end{align} $$
$$ \begin{align} \sum_{i=0}^{p-1}\sum_{j=0}^{p-1}A_{i,j}\equiv \bigg(\frac{p}{3}\bigg)\pmod{p}. \end{align} $$
The first author [Reference Liu8] confirmed the conjectural congruence (1.3) using combinatorial identities which were proved by Zeilberger’s algorithm [Reference Petkovšek, Wilf and Zeilberger10].
It is natural to consider the q-counterpart for
![]() $A_{n,m}$
. The q-super Catalan numbers are defined as
$A_{n,m}$
. The q-super Catalan numbers are defined as
where the q-factorial
![]() $[n]!=\prod _{k=1}^n(1-q^k)/(1-q)$
. Warnaar and Zudilin [Reference Warnaar and Zudilin16] obtained the remarkable result that the
$[n]!=\prod _{k=1}^n(1-q^k)/(1-q)$
. Warnaar and Zudilin [Reference Warnaar and Zudilin16] obtained the remarkable result that the
![]() $A_{n,m}(q)$
are polynomials with nonnegative coefficients (positive polynomials) and Guo et al. [Reference Guo, Jouhet and Zeng7] obtained another interesting positivity result related to
$A_{n,m}(q)$
are polynomials with nonnegative coefficients (positive polynomials) and Guo et al. [Reference Guo, Jouhet and Zeng7] obtained another interesting positivity result related to
![]() $A_{n,m}(q)$
.
$A_{n,m}(q)$
.
As mentioned in [Reference Warnaar and Zudilin16], one can obtain a q-analogue of Von Szily’s identity (1.2),
 $$ \begin{align} A_{n,m}(q)=\sum_{k=-\infty}^{\infty}(-1)^kq^{{k\choose 2}+k^2}{2n\brack n+k}{2m\brack m+k}, \end{align} $$
$$ \begin{align} A_{n,m}(q)=\sum_{k=-\infty}^{\infty}(-1)^kq^{{k\choose 2}+k^2}{2n\brack n+k}{2m\brack m+k}, \end{align} $$
by taking
![]() $(a,b,c)\mapsto (1,\infty , q^{-m})$
in the very-well poised
$(a,b,c)\mapsto (1,\infty , q^{-m})$
in the very-well poised
![]() $_6\phi _5$
summation [Reference Gasper and Rahman5, (II.21)]. Here and throughout the paper, the q-binomial coefficients are defined as
$_6\phi _5$
summation [Reference Gasper and Rahman5, (II.21)]. Here and throughout the paper, the q-binomial coefficients are defined as
 $$ \begin{align*} {n\brack k} =\begin{cases} \displaystyle\frac{(q;q)_n}{(q;q)_k(q;q)_{n-k}} &\text{if }0\leqslant k\leqslant n,\\[10pt] 0 &\text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*} {n\brack k} =\begin{cases} \displaystyle\frac{(q;q)_n}{(q;q)_k(q;q)_{n-k}} &\text{if }0\leqslant k\leqslant n,\\[10pt] 0 &\text{otherwise,} \end{cases} \end{align*} $$
where the q-shifted factorials are given by
![]() $(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for
$(a;q)_n=(1-a)(1-aq)\cdots (1-aq^{n-1})$
for
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $(a;q)_0=1$
. The nth cyclotomic polynomial is given by
$(a;q)_0=1$
. The nth cyclotomic polynomial is given by
 $$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\le k \le n\\[3pt](n,k)=1}} (q-\zeta^k), \end{align*} $$
$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\le k \le n\\[3pt](n,k)=1}} (q-\zeta^k), \end{align*} $$
where
![]() $\zeta $
denotes a primitive nth root of unity.
$\zeta $
denotes a primitive nth root of unity.
Our interest concerns a q-analogue of Apagodu’s congruence (1.3) as follows.
Theorem 1.1. For any positive integer n, modulo
![]() $\Phi_n(q)$
,
$\Phi_n(q)$
,
 $$ \begin{align} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) \equiv \begin{cases} \displaystyle\bigg(\frac{n}{3}\bigg)q^{n-1}\quad&\text{if }n\not\equiv 0\pmod{3}\\ q^{n/3-1}(1-q^{n/3})\quad&\text{if }n\equiv 0\pmod{3}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) \equiv \begin{cases} \displaystyle\bigg(\frac{n}{3}\bigg)q^{n-1}\quad&\text{if }n\not\equiv 0\pmod{3}\\ q^{n/3-1}(1-q^{n/3})\quad&\text{if }n\equiv 0\pmod{3}. \end{cases} \end{align} $$
We remark that letting
![]() $n=p$
and
$n=p$
and
![]() $q\to 1$
in (1.5) leads us to (1.3). The proof of (1.5) relies on (1.4) and the following q-congruence due to Tauraso [Reference Tauraso14, Corollary 4.3]:
$q\to 1$
in (1.5) leads us to (1.3). The proof of (1.5) relies on (1.4) and the following q-congruence due to Tauraso [Reference Tauraso14, Corollary 4.3]:
 $$ \begin{align} \sum_{i=0}^{n-1}q^i{2i\brack i+k}\equiv \bigg(\frac{n-k}{3}\bigg)q^{3r(r+1)/2+k(2r+1)}\pmod{\Phi_n(q)}, \end{align} $$
$$ \begin{align} \sum_{i=0}^{n-1}q^i{2i\brack i+k}\equiv \bigg(\frac{n-k}{3}\bigg)q^{3r(r+1)/2+k(2r+1)}\pmod{\Phi_n(q)}, \end{align} $$
where k is a nonnegative integer and
![]() $r=\lfloor 2(n-k)/3\rfloor $
.
$r=\lfloor 2(n-k)/3\rfloor $
.
As we will see, the proof of (1.5) is more natural than that of (1.3) in [Reference Liu8] and avoids using some exotic combinatorial identities. We shall present the proof of Theorem 1.1 in the next section.
2 Proof of Theorem 1.1
By (1.4),
 $$ \begin{align} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) & =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}\sum_{k=-j}^j(-1)^kq^{{k\choose 2}+k^2}{2j\brack \,j+k}{2i\brack i+k}\notag\\ &=\sum_{k=1-n}^{n-1}(-1)^kq^{{k\choose 2}+k^2}\sum_{i=0}^{n-1}q^i{2i\brack i+k}\sum_{j=0}^{n-1}q^{j}{2j\brack \,j+k}\notag\\ &=\sum_{k=1-n}^{n-1}(-1)^kq^{{k\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2. \end{align} $$
$$ \begin{align} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) & =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}\sum_{k=-j}^j(-1)^kq^{{k\choose 2}+k^2}{2j\brack \,j+k}{2i\brack i+k}\notag\\ &=\sum_{k=1-n}^{n-1}(-1)^kq^{{k\choose 2}+k^2}\sum_{i=0}^{n-1}q^i{2i\brack i+k}\sum_{j=0}^{n-1}q^{j}{2j\brack \,j+k}\notag\\ &=\sum_{k=1-n}^{n-1}(-1)^kq^{{k\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2. \end{align} $$
Let
 $$ \begin{align*} a(k)=(-1)^kq^{{k\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2 \end{align*} $$
$$ \begin{align*} a(k)=(-1)^kq^{{k\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2 \end{align*} $$
and
 $$ \begin{align*} b(k)=a(-k)=(-1)^kq^{{k+1\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2. \end{align*} $$
$$ \begin{align*} b(k)=a(-k)=(-1)^kq^{{k+1\choose 2}+k^2}\bigg(\sum_{i=0}^{n-1}q^i{2i\brack i+k}\bigg)^2. \end{align*} $$
We split the sum on the right-hand side of (2.1) into two pieces:
 $$ \begin{align*} S_1=\sum_{k=0}^{n-1}a(k)\quad \text{and}\quad S_2=\sum_{k=1}^{n-1}b(k), \end{align*} $$
$$ \begin{align*} S_1=\sum_{k=0}^{n-1}a(k)\quad \text{and}\quad S_2=\sum_{k=1}^{n-1}b(k), \end{align*} $$
so that
 $$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)=S_1+S_2. \end{align} $$
$$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)=S_1+S_2. \end{align} $$
From (1.6), we deduce that
and
where
![]() $r=\lfloor 2(n-k)/3\rfloor $
.
$r=\lfloor 2(n-k)/3\rfloor $
.
Next, we shall distinguish three cases to prove (1.5).
Case 1:
![]() $n\equiv 1\pmod {3}$
.
$n\equiv 1\pmod {3}$
.
If
![]() $k=3m$
, then
$k=3m$
, then
![]() $ (({n-k})/{3})=1$
and
$ (({n-k})/{3})=1$
and
![]() $r=2(n-1)/3-2m$
. It follows from (2.3) and (2.4) that
$r=2(n-1)/3-2m$
. It follows from (2.3) and (2.4) that
and
If
![]() $k=3m+1$
, then
$k=3m+1$
, then
![]() $ (({n-k})/{3})=0$
, and so
$ (({n-k})/{3})=0$
, and so
If
![]() $k=3m+2$
, then
$k=3m+2$
, then
![]() $ (({n-k})/{3})=-1$
and
$ (({n-k})/{3})=-1$
and
![]() $r=2(n-1)/3-2m-1$
, and so
$r=2(n-1)/3-2m-1$
, and so
and
Combining (2.5)–(2.9) gives modulo
![]() $\Phi_n(q)$
,
$\Phi_n(q)$
,
 $$ \begin{align} a(k)\equiv \begin{cases} (-1)^mq^{2(2n+1)(n-1)/3+3m(m-1)/2}\quad &\text{if }k=3m \\ 0\quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n+1)/3+(m+1)(3m-2)/2}\quad &\text{if }k=3m+2 \end{cases} \end{align} $$
$$ \begin{align} a(k)\equiv \begin{cases} (-1)^mq^{2(2n+1)(n-1)/3+3m(m-1)/2}\quad &\text{if }k=3m \\ 0\quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n+1)/3+(m+1)(3m-2)/2}\quad &\text{if }k=3m+2 \end{cases} \end{align} $$
and
 $$ \begin{align} b(k)\equiv \begin{cases} (-1)^mq^{2(2n+1)(n-1)/3+3m(m+1)/2}\quad &\text{if }k=3m\\ 0\quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n+1)/3+(m+2)(3m+1)/2}\quad &\text{if }k=3m+2. \end{cases} \end{align} $$
$$ \begin{align} b(k)\equiv \begin{cases} (-1)^mq^{2(2n+1)(n-1)/3+3m(m+1)/2}\quad &\text{if }k=3m\\ 0\quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n+1)/3+(m+2)(3m+1)/2}\quad &\text{if }k=3m+2. \end{cases} \end{align} $$
It follows from (2.10) and (2.11) that
 $$ \begin{align} S_1=\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\notag\\ &\equiv q^{2(2n+1)(n-1)/3}\sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2}\notag\\ &\quad +q^{2n(2n+1)/3}\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+1)(3m-2)/2}\pmod{\Phi_n(q)} \end{align} $$
$$ \begin{align} S_1=\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\notag\\ &\equiv q^{2(2n+1)(n-1)/3}\sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2}\notag\\ &\quad +q^{2n(2n+1)/3}\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+1)(3m-2)/2}\pmod{\Phi_n(q)} \end{align} $$
and
 $$ \begin{align} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\notag\\ &\equiv q^{2(2n+1)(n-1)/3}\sum_{m=1}^{ (n-1)/3}(-1)^mq^{3m(m+1)/2} \notag\\ &\quad +q^{2n(2n+1)/3}\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}\pmod{\Phi_n(q)}. \end{align} $$
$$ \begin{align} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\notag\\ &\equiv q^{2(2n+1)(n-1)/3}\sum_{m=1}^{ (n-1)/3}(-1)^mq^{3m(m+1)/2} \notag\\ &\quad +q^{2n(2n+1)/3}\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}\pmod{\Phi_n(q)}. \end{align} $$
Combining (2.2), (2.12) and (2.13), we arrive at
 $$ \begin{align*} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)\\ &\quad\equiv q^{2(2n+1)(n-1)/3}\bigg(\sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2}+\sum_{m=1}^{ (n-1)/3}(-1)^mq^{3m(m+1)/2}\bigg)\\ &\qquad +q^{2n(2n+1)/3}\bigg(\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+1)(3m-2)/2}+\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}\bigg) \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)\\ &\quad\equiv q^{2(2n+1)(n-1)/3}\bigg(\sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2}+\sum_{m=1}^{ (n-1)/3}(-1)^mq^{3m(m+1)/2}\bigg)\\ &\qquad +q^{2n(2n+1)/3}\bigg(\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+1)(3m-2)/2}+\sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}\bigg) \pmod{\Phi_n(q)}. \end{align*} $$
Noting that
 $$ \begin{align*} \sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2} =-\sum_{m=-1}^{ (n-4)/3}(-1)^mq^{3m(m+1)/2} \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{ (n-1)/3}(-1)^mq^{3m(m-1)/2} =-\sum_{m=-1}^{ (n-4)/3}(-1)^mq^{3m(m+1)/2} \end{align*} $$
and
 $$ \begin{align*} \sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}= -\sum_{m=1}^{ (n-1)/3}(-1)^{m}q^{(m+1)(3m-2)/2}, \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{ (n-4)/3}(-1)^mq^{(m+2)(3m+1)/2}= -\sum_{m=1}^{ (n-1)/3}(-1)^{m}q^{(m+1)(3m-2)/2}, \end{align*} $$
we obtain
 $$ \begin{align*} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) &\equiv q^{2n(2n+1)/3-1}-(-1)^{{(n-1)}/{3}}q^{(n+1)(3n-2)/2}+(-1)^{{(n-1)}/{3}}q^{(n-1)(3n+2)/2}\\ &=q^{2n(2n+1)/3-1}+(-1)^{(n-1)/3}q^{(n-1)(3n+2)/2}(1-q^n)\\ &\equiv q^{-1} \equiv q^{n-1} \pmod{\Phi_n(q)}, \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) &\equiv q^{2n(2n+1)/3-1}-(-1)^{{(n-1)}/{3}}q^{(n+1)(3n-2)/2}+(-1)^{{(n-1)}/{3}}q^{(n-1)(3n+2)/2}\\ &=q^{2n(2n+1)/3-1}+(-1)^{(n-1)/3}q^{(n-1)(3n+2)/2}(1-q^n)\\ &\equiv q^{-1} \equiv q^{n-1} \pmod{\Phi_n(q)}, \end{align*} $$
where we have used the fact
![]() $q^n\equiv 1\pmod {\Phi _n(q)}$
. This completes the proof of the case
$q^n\equiv 1\pmod {\Phi _n(q)}$
. This completes the proof of the case
![]() $n\equiv 1\pmod {3}$
of (1.5).
$n\equiv 1\pmod {3}$
of (1.5).
Case 2:
![]() $n\equiv 2\pmod {3}$
.
$n\equiv 2\pmod {3}$
.
By using the same method as in the previous case, we can evaluate
![]() $a(k)$
and
$a(k)$
and
![]() $b(k)$
modulo
$b(k)$
modulo
![]() $\Phi _n(q)$
:
$\Phi _n(q)$
:
 $$ \begin{align*} a(k)\equiv \begin{cases} (-1)^mq^{2(2n-1)(n+1)/3+3m(m-1)/2}\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n-1)/3+(3m+2)(m-1)/2}\quad &\text{if }k=3m+1\\ 0\quad &\text{if }k=3m+2 \end{cases} \end{align*} $$
$$ \begin{align*} a(k)\equiv \begin{cases} (-1)^mq^{2(2n-1)(n+1)/3+3m(m-1)/2}\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n-1)/3+(3m+2)(m-1)/2}\quad &\text{if }k=3m+1\\ 0\quad &\text{if }k=3m+2 \end{cases} \end{align*} $$
and
 $$ \begin{align*} b(k)\equiv \begin{cases} (-1)^mq^{2(2n-1)(n+1)/3+3m(m+1)/2}\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n-1)/3+(3m+5)m/2}\quad &\text{if }k=3m+1\\ 0\quad &\text{if }k=3m+2. \end{cases} \end{align*} $$
$$ \begin{align*} b(k)\equiv \begin{cases} (-1)^mq^{2(2n-1)(n+1)/3+3m(m+1)/2}\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n-1)/3+(3m+5)m/2}\quad &\text{if }k=3m+1\\ 0\quad &\text{if }k=3m+2. \end{cases} \end{align*} $$
It follows that
 $$ \begin{align*} S_1=\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\\ &\equiv q^{2(2n-1)(n+1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2} \\ &\quad -q^{2n(2n-1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}\pmod{\Phi_n(q)} \end{align*} $$
$$ \begin{align*} S_1=\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\\ &\equiv q^{2(2n-1)(n+1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2} \\ &\quad -q^{2n(2n-1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}\pmod{\Phi_n(q)} \end{align*} $$
and
 $$ \begin{align*} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\\ &\equiv q^{2(2n-1)(n+1)/3}\sum_{m=1}^{ (n-2)/3}(-1)^mq^{3m(m+1)/2} \\ &\quad -q^{2n(2n-1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+5)m/2} \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\\ &\equiv q^{2(2n-1)(n+1)/3}\sum_{m=1}^{ (n-2)/3}(-1)^mq^{3m(m+1)/2} \\ &\quad -q^{2n(2n-1)/3}\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+5)m/2} \pmod{\Phi_n(q)}. \end{align*} $$
Thus,
 $$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)=S_1+S_2\notag\\ &\quad\equiv q^{2(2n-1)(n+1)/3}\bigg(\sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2}+\sum_{m=1}^{ (n-2)/3}(-1)^mq^{3m(m+1)/2}\bigg)\notag\\ &\qquad-q^{2n(2n-1)/3}\bigg(\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}+\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+5)m/2}\bigg)\pmod{\Phi_n(q)}. \end{align} $$
$$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q)=S_1+S_2\notag\\ &\quad\equiv q^{2(2n-1)(n+1)/3}\bigg(\sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2}+\sum_{m=1}^{ (n-2)/3}(-1)^mq^{3m(m+1)/2}\bigg)\notag\\ &\qquad-q^{2n(2n-1)/3}\bigg(\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}+\sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+5)m/2}\bigg)\pmod{\Phi_n(q)}. \end{align} $$
Furthermore, note that
 $$ \begin{align} \sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2}=-\sum_{m=-1}^{ (n-5)/3}(-1)^mq^{3m(m+1)2} \end{align} $$
$$ \begin{align} \sum_{m=0}^{ (n-2)/3}(-1)^mq^{3m(m-1)/2}=-\sum_{m=-1}^{ (n-5)/3}(-1)^mq^{3m(m+1)2} \end{align} $$
and
 $$ \begin{align} \sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}= -\sum_{m=-1}^{ (n-5)/3}(-1)^mq^{(3m+5)m/2}. \end{align} $$
$$ \begin{align} \sum_{m=0}^{ (n-2)/3}(-1)^mq^{(3m+2)(m-1)/2}= -\sum_{m=-1}^{ (n-5)/3}(-1)^mq^{(3m+5)m/2}. \end{align} $$
 $$ \begin{align*} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) &\equiv (-1)^{(n-2)/3}q^{(n+1)(3n-2)/2}-q^{2n(2n-1)/3-1}-(-1)^{(n-2)/3}q^{(3n+2)(n-1)/2} \\ &=-q^{2n(2n-1)/3-1}+(-1)^{(n-2)/3}q^{(3n+2)(n-1)/2}(q^n-1) \\ &\equiv -q^{-1} \equiv -q^{n-1} \pmod{\Phi_n(q)}, \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) &\equiv (-1)^{(n-2)/3}q^{(n+1)(3n-2)/2}-q^{2n(2n-1)/3-1}-(-1)^{(n-2)/3}q^{(3n+2)(n-1)/2} \\ &=-q^{2n(2n-1)/3-1}+(-1)^{(n-2)/3}q^{(3n+2)(n-1)/2}(q^n-1) \\ &\equiv -q^{-1} \equiv -q^{n-1} \pmod{\Phi_n(q)}, \end{align*} $$
which is the case
![]() $n\equiv 2\pmod {3}$
of (1.5).
$n\equiv 2\pmod {3}$
of (1.5).
Case 3:
![]() $n\equiv 0\pmod {3}$
.
$n\equiv 0\pmod {3}$
.
By using the same method as in the first case, we find that modulo
![]() $\Phi_n(q)$
,
$\Phi_n(q)$
,
 $$ \begin{align*} a(k) \equiv \begin{cases} 0\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n+1)/3+(3m+2)(m-1)/2} \quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n-1)/3+(3m-2)(m+1)/2} \quad &\text{if }k=3m+2 \end{cases} \end{align*} $$
$$ \begin{align*} a(k) \equiv \begin{cases} 0\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n+1)/3+(3m+2)(m-1)/2} \quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n-1)/3+(3m-2)(m+1)/2} \quad &\text{if }k=3m+2 \end{cases} \end{align*} $$
and
 $$ \begin{align*} b(k)\equiv\begin{cases} 0\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n+1)/3+m(3m+5)/2} \quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n-1)/3+(m+2)(3m+1)/2} \quad &\text{if }k=3m+2. \end{cases} \end{align*} $$
$$ \begin{align*} b(k)\equiv\begin{cases} 0\quad &\text{if }k=3m\\ (-1)^{m+1}q^{2n(2n+1)/3+m(3m+5)/2} \quad &\text{if }k=3m+1\\ (-1)^mq^{2n(2n-1)/3+(m+2)(3m+1)/2} \quad &\text{if }k=3m+2. \end{cases} \end{align*} $$
It follows that
 $$ \begin{align*} S_1 =\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\\ &\equiv q^{2n(2n-1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m-2)(m+1)/2} \\ &\quad -q^{2n(2n+1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m+2)(m-1)/2} \pmod{\Phi_n(q)} \end{align*} $$
$$ \begin{align*} S_1 =\sum_{k=0}^{n-1}a(k) &=\sum_{m=0}^{\lfloor (n-1)/3\rfloor}a(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}a(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}a(3m+2)\\ &\equiv q^{2n(2n-1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m-2)(m+1)/2} \\ &\quad -q^{2n(2n+1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m+2)(m-1)/2} \pmod{\Phi_n(q)} \end{align*} $$
and
 $$ \begin{align*} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\\ &\equiv q^{2n(2n-1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(m+2)(3m+1)/2} \\ &\quad -q^{2n(2n+1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{m(3m+5)/2} \pmod{\Phi_n(q)}. \end{align*} $$
$$ \begin{align*} S_2=\sum_{k=1}^{n-1}b(k) &=\sum_{m=1}^{\lfloor (n-1)/3\rfloor}b(3m)+\sum_{m=0}^{\lfloor (n-2)/3\rfloor}b(3m+1)+\sum_{m=0}^{\lfloor (n-3)/3\rfloor}b(3m+2)\\ &\equiv q^{2n(2n-1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(m+2)(3m+1)/2} \\ &\quad -q^{2n(2n+1)/3}\sum_{m=0}^{ (n-3)/3}(-1)^mq^{m(3m+5)/2} \pmod{\Phi_n(q)}. \end{align*} $$
Thus,
 $$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) =S_1+S_2\notag\\ &\quad\equiv q^{2n(2n-1)/3}\bigg(\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m-2)(m+1)/2}+\sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(m+2)(3m+1)}/{2}}\bigg)\notag\\ &\qquad-q^{2n(2n+1)/3}\bigg(\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m+2)(m-1)/2}+\sum_{m=0}^{ (n-3)/3}(-1)^mq^{{m(3m+5)}/{2}}\bigg) \pmod{\Phi_n(q)}. \end{align} $$
$$ \begin{align} &\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) =S_1+S_2\notag\\ &\quad\equiv q^{2n(2n-1)/3}\bigg(\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m-2)(m+1)/2}+\sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(m+2)(3m+1)}/{2}}\bigg)\notag\\ &\qquad-q^{2n(2n+1)/3}\bigg(\sum_{m=0}^{ (n-3)/3}(-1)^mq^{(3m+2)(m-1)/2}+\sum_{m=0}^{ (n-3)/3}(-1)^mq^{{m(3m+5)}/{2}}\bigg) \pmod{\Phi_n(q)}. \end{align} $$
Furthermore, note that
 $$ \begin{align} \sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(3m+2)(m-1)}/{2}}=-\sum_{m=-1}^{ (n-6)/3}(-1)^mq^{{m(3m+5)}/{2}} \end{align} $$
$$ \begin{align} \sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(3m+2)(m-1)}/{2}}=-\sum_{m=-1}^{ (n-6)/3}(-1)^mq^{{m(3m+5)}/{2}} \end{align} $$
and
 $$ \begin{align} \sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(3m-2)(m+1)}/{2}}= -\sum_{m=-1}^{ (n-6)/3}(-1)^mq^{{(3m+1)(m+2)}/{2}}. \end{align} $$
$$ \begin{align} \sum_{m=0}^{ (n-3)/3}(-1)^mq^{{(3m-2)(m+1)}/{2}}= -\sum_{m=-1}^{ (n-6)/3}(-1)^mq^{{(3m+1)(m+2)}/{2}}. \end{align} $$
Finally, combining (2.17)–(2.19), we arrive at
 $$ \begin{align*} \sum_{i=0}^{n-1} & \sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) \\ &\equiv q^{{2n(2n-1)}/{3}-1}-q^{{2n(2n+1)}/{3}-1}+(-1)^{{n}/{3}}q^{{(n+1)(3n-2)}/{2}} +(-1)^{{(n-3)}/{3}}q^{{(n-1)(3n+2)}/{2}}\\ &=q^{{n(4n-3)}/{3}+{n}/{3}-1}(1-q^{n+{n}/{3}})-(-1)^{{n}/{3}}q^{{(n-1)(3n+2)}/{2}}(1-q^n) \\ &\equiv q^{{n}/{3}-1}(1-q^{{n}/{3}}) \pmod{\Phi_n(q)}, \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n-1} & \sum_{j=0}^{n-1}q^{i+j}A_{i,j}(q) \\ &\equiv q^{{2n(2n-1)}/{3}-1}-q^{{2n(2n+1)}/{3}-1}+(-1)^{{n}/{3}}q^{{(n+1)(3n-2)}/{2}} +(-1)^{{(n-3)}/{3}}q^{{(n-1)(3n+2)}/{2}}\\ &=q^{{n(4n-3)}/{3}+{n}/{3}-1}(1-q^{n+{n}/{3}})-(-1)^{{n}/{3}}q^{{(n-1)(3n+2)}/{2}}(1-q^n) \\ &\equiv q^{{n}/{3}-1}(1-q^{{n}/{3}}) \pmod{\Phi_n(q)}, \end{align*} $$
which confirms the case
![]() $n\equiv 0\pmod {3}$
of (1.5).
$n\equiv 0\pmod {3}$
of (1.5).