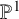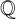ON THE FIBRES OF AN ELLIPTIC SURFACE WHERE THE RANK DOES NOT JUMP

Abstract

For a nonconstant elliptic surface over $\mathbb {P}^1$ defined over $\mathbb {Q}$, it is a result of Silverman [‘Heights and the specialization map for families of abelian varieties’, J. reine angew. Math. 342 (1983), 197–211] that the Mordell–Weil rank of the fibres is at least the rank of the group of sections, up to finitely many fibres. If the elliptic surface is nonisotrivial, one expects that this bound is an equality for infinitely many fibres, although no example is known unconditionally. Under the Bunyakovsky conjecture, such an example has been constructed by Neumann [‘Elliptische Kurven mit vorgeschriebenem Reduktionsverhalten. I’, Math. Nachr. 49 (1971), 107–123] and Setzer [‘Elliptic curves of prime conductor’, J. Lond. Math. Soc. (2) 10 (1975), 367–378]. In this note, we show that the Legendre elliptic surface has the desired property, conditional on the existence of infinitely many Mersenne primes.

1 Introduction

Let $\pi :X\to \mathbb {P}^1$ be a nonconstant elliptic surface (with section) defined over $\mathbb {Q}$ and let $\mathrm {MW}(X,\pi )$ be its group of sections defined over $\mathbb {Q}$ . This group is finitely generated by the Lang–Néron theorem [7]. By a theorem of Silverman [16], for all but finitely many $b\in \mathbb {P}^1(\mathbb {Q})$ , the fibre $X_b$ is an elliptic curve with $\mathrm {rk}\, X_b(\mathbb {Q})\ge \mathrm {rk}\, \mathrm {MW}(X,\pi )$ and one can ask when is this inequality strict and when is it an equality. Thus, let us define

$$ \begin{align*} \mathscr{J}(X,\pi)=\{b\in \mathbb{P}^1(\mathbb{Q}) : X_b\mbox{ is an elliptic curve with }\mathrm{rk}\, X_b(\mathbb{Q})>\mathrm{rk}\, \mathrm{MW}(X,\pi)\} \end{align*} $$

and

$$ \begin{align*} \mathscr{N}(X,\pi)=\{b\in \mathbb{P}^1(\mathbb{Q}) : X_b\mbox{ is an elliptic curve with }\mathrm{rk}\, X_b(\mathbb{Q})=\mathrm{rk}\, \mathrm{MW}(X,\pi)\}. \end{align*} $$

These are the sets of points $b\in \mathbb {P}^1(\mathbb {Q})$ where the rank jumps and where it does not jump, respectively. The question is whether these sets are infinite. There is a considerable body of work addressing this problem for $\mathscr {J}(X,\pi )$ and we refer the reader to [13] and the references therein.

However, much less is known for $\mathscr {N}(X,\pi )$ . In [2], Cassels and Schinzel produced an example where $\mathscr {N}(X,\pi )$ is empty, conditional on a conjecture of Selmer. Regarding the infinitude of $\mathscr {N}(X,\pi )$ , there are plenty of results where this set is infinite for quadratic twist families (see [8] for a survey on recent results). The example of Cassels and Schinzel, as well as quadratic twist families, are isotrivial.

In the nonisotrivial case, one expects the following result.

Conjecture 1.1. If $\pi :X\to \mathbb {P}^1$ is nonisotrivial, then both $\mathscr {J}(X,\pi )$ and $\mathscr {N}(X,\pi )$ are infinite.

A heuristic for this conjecture is implicit in Appendix A of [3]. We revisit this heuristic in Section 4.1 for the convenience of the reader.

Let us consider the case when $\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$ . Such elliptic surfaces over $\mathbb {Q}$ are abundant (see for instance [6]). Regarding the infinitude of $\mathscr {N}(X,\pi )$ , the following assertion is a very special case of Conjecture 1.1.

Conjecture 1.2. Let $\pi :X\to \mathbb {P}^1$ be a nonisotrivial elliptic surface defined over $\mathbb {Q}$ with the property that $\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$ . Then there are infinitely many $b\in \mathbb {P}^1(\mathbb {Q})$ with $\mathrm {rk}\, X_b(\mathbb {Q})=0$ . That is, $\mathscr {N}(X,\pi )$ is infinite.

This problem remains open and, to the best of our knowledge, not a single example of a nonisotrivial elliptic surface with an infinite $\mathscr {N}(X,\pi )$ is known. Nevertheless, let us consider the elliptic surface $\pi :S\to \mathbb {P}^1$ defined by the Weierstrass equation:

$$ \begin{align*} y^2 = x^3 + tx^2-16x, \end{align*} $$

where t is an affine coordinate on $\mathbb {P}^1$ . This elliptic surface is nonisotrivial and it was first studied by Neumann [10] and Setzer [15] (see also [18]). If p is a prime of the form $p=b^2+64$ for an integer $b\equiv 3\bmod 4$ , then $S_b(\mathbb {Q})\simeq \mathbb {Z}/2\mathbb {Z}$ and in particular $S_b$ has rank $0$ over $\mathbb {Q}$ . A well-known conjecture of Bunyakovsky predicts that there are infinitely many primes p of this form, so one gets a conditional example where Conjecture 1.2 holds.

In this note, we consider instead the Legendre elliptic surface $\pi :Y\to \mathbb {P}^1$ defined by the Weierstrass equation:

$$ \begin{align*} y^2 = x(x+1)(x+t). \end{align*} $$

This elliptic surface has $\mathrm {rk}\,\mathrm {MW}(Y,\pi )=0$ (see Lemma 2.2). To state our main result, let us recall that a Mersenne prime is a prime number p of the form $p=2^q-1$ with q a prime. It is conjectured that there are infinitely many of them (see Section 4.2 for details). We prove the following result.

Theorem 1.3. Let $q\ge 5$ be a prime such that $p=2^q-1$ is a Mersenne prime. Then the elliptic curve $E_q$ defined by $y^2=x(x+1)(x+2^q)$ has $\mathrm {rk}\, E_q(\mathbb {Q})=0$ .

In particular, if there are infinitely Mersenne primes, then the (nonisotrivial) Legendre elliptic surface $\pi :Y\to \mathbb {P}^1$ has the property that $\mathscr {N}(Y,\pi )$ is infinite.

The proof of Theorem 1.3 has two main ingredients. First, using a descent bound, we show that $\mathrm {rk}\, E_q(\mathbb {Q})\le 1$ , which falls short of proving the result. However, using known cases of the parity conjecture due to Monsky [9] as well as some control on Shafarevich–Tate groups, we deduce that $\mathrm {rk}\, E_q(\mathbb {Q})=1$ is not possible. For this strategy to work, we need to carefully analyse the reduction type of $E_q$ at the primes $2$ and p.

Finally, let us mention a somewhat unexpected motivation for Conjecture 1.2. Although we have only discussed elliptic surfaces over $\mathbb {Q}$ , Conjecture 1.2 can also be formulated over number fields. In [12], it is shown that this conjecture over number fields implies that for every number field K, the analogue of Hilbert’s tenth problem for the ring of integers $O_K$ is undecidable.

2 Preliminaries

2.1 The Legendre elliptic surface

Let t be the affine coordinate on $\mathbb {P}^1$ . The Legendre elliptic surface is the (relatively minimal) elliptic surface $\pi :Y\to \mathbb {P}^1$ defined over $\mathbb {Q}$ by the affine Weierstrass equation:

$$ \begin{align*} y^2=x(x+1)(x+t). \end{align*} $$

We refer the reader to [20] for a detailed study of this elliptic surface. The first lemma is a direct computation.

Lemma 2.1. The Legendre elliptic surface is nonisotrivial and rational. It has three singular fibres: at $t=0$ of Kodaira type $I_2$ , at $t=-1$ of Kodaira type $I_2$ and at $t=\infty $ of Kodaira type $I_2^*$ .

Using this, we get the next lemma.

Lemma 2.2. We have $\mathrm {rk}\, \mathrm {MW}(Y,\pi )=0$ . In fact, the group of sections over $\mathbb {C}$ is formed by the $2$ -torsion sections.

Proof. Let us base change to $\mathbb {C}$ . Since $\pi :Y_{\mathbb {C}}\to \mathbb {P}^1$ is a rational elliptic surface with singular fibres of types $I_2$ , $I_2$ and $I_2^*$ , its group of sections is given in the entry 71 of the main theorem of [11].

2.2 Bounds for the rank

The following result is a more precise version of the bound provided by [1, Proposition 1.3]; the argument is a variation of the proof of [1, Lemma 3.1].

Theorem 2.3. Let E be an elliptic curve over $\mathbb {Q}$ admitting a $2$ -isogeny $\theta :E\to E'$ over $\mathbb {Q}$ . Let $\alpha $ and $\mu $ be the number of places of additive and of multiplicative reduction of E, respectively. Then,

$$ \begin{align*} \mathrm{rk}\, E(\mathbb{Q})\le 2\alpha +\mu-1. \end{align*} $$

If equality holds, then the $2$ -primary part of the Shafarevich–Tate group is trivial.

Proof. The claimed bound is precisely [1, Proposition 1.3]. Suppose that equality holds. We will show that the $2$ -torsion part of is trivial, which is sufficient.

Let $S_2(E)$ be the $2$ -Selmer group of E. Then we have the exact sequence

and we see that it suffices to show

(2.1) $$ \begin{align} 2\alpha+\mu-1 + \dim_{\mathbb{F}_2}E(\mathbb{Q})[2]\ge \dim_{\mathbb{F}_2} S_2(E) \end{align} $$

because $\dim _{\mathbb {F}_2}E(\mathbb {Q})/2E(\mathbb {Q}) = \mathrm {rk}\, E(\mathbb {Q}) + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]=2\alpha +\mu -1 + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]$ .

Let $\theta :E\to E'$ be a rational $2$ -isogeny and let $\theta ':E'\to E$ be its dual. For the corresponding Selmer groups $S_\theta (E)$ and $S_{\theta '}(E)$ ,

(2.2) $$ \begin{align} \dim_{\mathbb{F}_2} S_{\theta}(E) + \dim_{\mathbb{F}_2} S_{\theta'}(E') \le 2\alpha + \mu+1 \end{align} $$

(see [1, Theorem 2.2]). These Selmer groups are related to $S_2(E)$ via the exact sequence

(2.3) $$ \begin{align} 0\to E'(\mathbb{Q})[\theta']/\theta(E(\mathbb{Q})[2])\to S_{\theta}(E)\to S_2(E)\to S_{\theta'}(E'), \end{align} $$

(see [14, Lemma 6.1]; note that although this is only claimed for odd primes p in [14], the hypothesis $p>2$ is not really needed at this point).

Let us consider two cases. First, let us assume that $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$ . Then (2.2) and (2.3) give

$$ \begin{align*} \dim_{\mathbb{F}_2} S_2(E)\le 2\alpha + \mu+1 - \dim_{\mathbb{F}_2} E'(\mathbb{Q})[\theta']/\theta(E(\mathbb{Q})[2]) =2\alpha + \mu, \end{align*} $$

where $\theta (E(\mathbb {Q})[2])=(0)$ because $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$ . This proves (2.1) when $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$ . Now let us assume $E(\mathbb {Q})[2]\simeq (\mathbb {Z}/2\mathbb {Z})^2$ . Then (2.2) and (2.3) directly give

$$ \begin{align*} \dim_{\mathbb{F}_2} S_2(E)\le 2\alpha + \mu+1, \end{align*} $$

which proves (2.1) in this case.

2.3 Root numbers

The root number $w(E)$ of an elliptic curve E over $\mathbb {Q}$ is the sign of the functional equation of E. Furthermore, one can define the local root number $w_p(E)$ at a prime p, and these local root numbers are related to $w(E)$ by

$$ \begin{align*}w(E)=-\prod_{p}w_p(E).\end{align*} $$

When E is semi-stable, we have a complete characterisation for the local root numbers:

$$ \begin{align*} w_p(E)= \begin{cases}1 & \mbox{if }E\mbox{ has good or nonsplit multiplicative reduction at }p,\\ -1 & \mbox{if }E\mbox{ has split multiplicative reduction at }p. \end{cases}\end{align*} $$

2.4 The parity conjecture

The following conjecture is an immediate consequence of the Birch and Swinnerton-Dyer conjecture.

Conjecture 2.4 (Parity conjecture).

Let E be an elliptic curve over $\mathbb {Q}$ . Then we have $(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$ .

The following result is a direct consequence of [9, Theorem 1.5].

Lemma 2.5. Let E be an elliptic curve over $\mathbb {Q}$ . If the $2$ -primary part of is finite, then $(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$ .

3 Proof of the main result

3.1 Reduction types

Lemma 3.1. Let $p=2^q-1$ be a Mersenne prime with $q\ge 5$ , and let $E_q$ be the elliptic curve defined by $y^2=x(x+1)(x+2^q)$ . Then, $E_q$ has split multiplicative reduction at $2$ , nonsplit multiplicative reduction at p and good reduction at all other primes.

Proof. [4, Lemma 1] implies that $E_q$ has multiplicative reduction at $2$ and p, and good reduction at every other prime. The reduction of $E_q$ modulo p is defined by

$$ \begin{align*} y^2=x(x+1)^2. \end{align*} $$

Replacing x by $x-1$ , we get the model $y^2=x^3-x^2$ with the singular point at $(x,y)=(0,0)$ . Thus, $E_q$ has split multiplicative reduction at p if and only if $\sqrt {-1}\in \mathbb {F}_p$ . Since

$$ \begin{align*}p= 2^q-1\equiv -1 \bmod 4,\end{align*} $$

we conclude that $E_q$ has nonsplit multiplicative reduction at p. However, the proof of [4, Lemma 2] yields the following minimal equation for $E_q$ over $\mathbb {Q}_2$ :

$$ \begin{align*} y^2+xy=x^3+2^{q-2}x+ 2^{q-4}x. \end{align*} $$

As $q\ge 5$ , the reduction modulo $2$ is given by the equation $y^2+xy=x^3$ , with the singular point at $(x,y)=(0,0)$ . This singular point is a nodal singularity with tangent slopes $0$ and $1$ , both defined over $\mathbb {F}_2$ . As a consequence, $E_q$ has split multiplicative reduction at $2$ .

3.2 Bounding the rank

Proof of Theorem 1.3.

By Lemma 3.1, the bad primes for $E_q$ are $2$ with split multiplicative reduction, and p with nonsplit multiplicative reduction. Therefore, $w(E)=1$ since $w_2(E)=-1$ and $w_p(E)=1$ .

Let us apply Theorem 2.3. We obtain $\mathrm {rk}\, E_q(\mathbb {Q})\leq 1$ and we claim that, in fact, $\mathrm {rk}\, E_q(\mathbb {Q})=0$ . For the sake of contradiction, assume that $\mathrm {rk}\, E_q(\mathbb {Q})= 1$ . Then, Theorem 2.3 implies that the $2$ -primary part of is trivial, and hence, by Lemma 2.5, we would obtain $w(E)=(-1)^{\mathrm {rk}\, E_q(\mathbb {Q})}=-1$ , which contradicts the fact that $w(E)=1$ .

4 Heuristics

4.1 On Conjecture 1.1

Let $\pi :X\to \mathbb {P}^1$ be a nonisotrivial elliptic surface defined over $\mathbb {Q}$ and let $R=\mathrm {rk}\, \mathrm {MW}(X,\pi )$ . Following the terminology in [3], the density conjecture of Silverman [17] asserts that

$$ \begin{align*} \mathrm{rk}\, X_b(\mathbb{Q})\in\{R,R+1\} \end{align*} $$

for all $b\in \mathbb {P}^1(\mathbb {Q})$ outside a set of density $0$ in $\mathbb {P}^1(\mathbb {Q})$ .

In [5], Helfgott proved that under some conjectures in analytic number theory, the average value of the root numbers $w(X_b)$ as b varies in $\mathbb {P}^1(\mathbb {Q})$ (ordered by height) exists and it is expressed in terms of local densities. As pointed out in [3, Appendix A, page 728], the conjectural value for this average of root numbers lies strictly between $-1$ and $1$ in the nonisotrivial case.

Therefore, under the previous conjectures, we deduce Conjecture 1.1 in a strong form: both sets $\mathscr {J}(X,\pi )$ and $\mathscr {N}(X,\pi )$ should have positive density in $\mathbb {P}^1(\mathbb {Q})$ .

4.2 On Mersenne primes

Let us recall the following folklore conjecture.

Conjecture 4.1. There are infinitely many Mersenne primes.

Mersenne primes provide a way to construct large prime numbers and considerable efforts are made to search for them, such as the Great Internet Mersenne Prime Search collaborative project [19].

Here we recall that the Lenstra–Pomerance–Wagstaff heuristic [21] suggests that the number of Mersenne primes $p=2^q-1$ in the interval $[1,x]$ is asymptotic to

$$ \begin{align*} \frac{e^{\gamma}}{\log 2}\log \log x, \end{align*} $$

where $\gamma $ is Euler’s constant. This gives a more precise form of Conjecture 4.1.