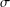Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T19:33:10.758Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE HYPERSTABILITY OF A PEXIDERISED $\unicode[STIX]{x1D70E}$-QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS

Published online by Cambridge University Press:  07 March 2018

IZ-IDDINE EL-FASSI  and
JANUSZ BRZDĘK
IZ-IDDINE EL-FASSI*
Affiliation:
Department of Mathematics, Faculty of Sciences, Ibn Tofail University, BP 133, Kenitra, Morocco email izidd-math@hotmail.fr
JANUSZ BRZDĘK
Affiliation:
Department of Mathematics, Pedagogical University, Podchorążych 2, 30-084 Kraków, Poland email jbrzdek@up.krakow.pl
*
✉izidd-math@hotmail.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by the notion of Ulam stability, we investigate some inequalities connected with the functional equation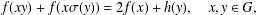

$$\begin{eqnarray}f(xy)+f(x\unicode[STIX]{x1D70E}(y))=2f(x)+h(y),\quad x,y\in G,\end{eqnarray}$$
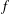for functions $f$ and 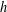$h$ mapping a semigroup 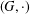$(G,\cdot )$ into a commutative semigroup 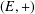$(E,+)$, where the map 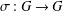$\unicode[STIX]{x1D70E}:G\rightarrow G$ is an endomorphism of 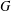$G$ with 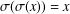$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70E}(x))=x$ for all 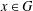$x\in G$. We derive from these results some characterisations of inner product spaces. We also obtain a description of solutions to the equation and hyperstability results for the 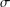$\unicode[STIX]{x1D70E}$-quadratic and 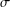$\unicode[STIX]{x1D70E}$-Drygas equations.

Keywords

hyperstability𝜎-quadratic functional equationsemigroupendomorphism of semigroup

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 39B52: Equations for functions with more general domains and/or ranges
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 459 - 470
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Aczél, J. and Dhombres, J. G., Functional Equations in Several Variables (Cambridge University Press, Cambridge, 1989).Google Scholar
Alsina, C., Sikorska, J. and Tomás, M. S., Norm Derivatives and Characterizations of Inner Product Spaces (World Scientific, Singapore, 2010).Google Scholar
Amir, D., Characterizations of Inner Product Spaces (Birkhäuser, Basel–Boston–Stuttgart, 1986).Google Scholar
Bahyrycz, A. and Olko, J., ‘On stability of the general linear equation’, Aequationes Math. 89 (2015), 1461–1476.Google Scholar
Bahyrycz, A. and Piszczek, M., ‘Hyperstability of the Jensen functional equation’, Acta Math. Hungar. 142 (2014), 353–365.Google Scholar
Bahyrycz, A. and Piszczek, M., ‘On approximately (p, q)-Wright affine functions and inner product spaces’, Acta Math. Sci. 36B(2) (2016), 593–601.Google Scholar
Baron, K., ‘On additive involutions and Hamel bases’, Aequationes Math. 87 (2014), 159–163.Google Scholar
Bouikhalene, B., Elqorachi, E. and Redouani, A., ‘Hyers–Ulam stability of the generalized quadratic functional equation in amenable semigroups’, J. Inequal. Pure Appl. Math. 8 (2007), Article ID 56, 18 pages.Google Scholar
Brillouët-Belluot, N., Brzdęk, J. and Ciepliński, K., ‘On some recent developments in Ulam’s type stability’, Abstr. Appl. Anal. 2012 (2012), Article ID 716936, 41 pages.Google Scholar
Brzdęk, J., ‘Remarks on stability of some inhomogeneous functional equations’, Aequationes Math. 89 (2015), 83–96.Google Scholar
Brzdęk, J. and Ciepliński, K., ‘Hyperstability and superstability’, Abstr. Appl. Anal. 2013 (2013), Article ID 401756, 13 pages.Google Scholar
Djoković, D. Ž., ‘A representation theorem for (X 1 - 1)(X 2 - 1)⋯(X n - 1) and its applications’, Ann. Polon. Math. 22 (1969), 189–198.Google Scholar
Drygas, H., ‘Quasi-inner products and their applications’, in: Advances in Multivariate Statistical Analysis (ed. Gupta, A. K.) (D. Reidel, Dordrecht, 1987), 13–30.Google Scholar
Ebanks, B. R., Kannappan, Pl. and Sahoo, P. K., ‘A common generalization of functional equations characterizing normed and quasi-inner product spaces’, Canad. Math. Bull. 35(3) (1992), 321–327.Google Scholar
Faǐziev, V. A. and Sahoo, P. K., ‘On Drygas functional equation on groups’, Int. J. Appl. Math. Stat. 7 (2007), 59–69.Google Scholar
Forti, G. L., ‘Hyers–Ulam stability of functional equations in several variables’, Aequationes Math. 50 (1995), 143–190.Google Scholar
Hyers, D. H., Isac, G. I. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhäuser, Basel, 1998).Google Scholar
Hyers, D. H. and Rassias, Th. M., ‘Approximate homomorphisms’, Aequationes Math. 44 (1992), 125–153.Google Scholar
Jordan, P. and von Neumann, J., ‘On inner products in linear, metric spaces’, Ann. of Math. (2) 36 (1935), 719–723.Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Mathematical Analysis (Hadronic Press, Palm Harbor, FL, 2001).Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis, Springer Optimization and its Applications, 48 (Springer, New York, 2011).Google Scholar
Kuczma, M., An Introduction to the Theory of Functional Equations and Inequalities. Cauchy’s Equation and Jensen’s Inequality (Birkhäuser, Basel, 2009).Google Scholar
Piszczek, M., ‘Remark on hyperstability of the general linear equation’, Aequationes Math. 88 (2014), 163–168.Google Scholar
Piszczek, M., ‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc. 52 (2015), 1827–1838.CrossRefGoogle Scholar
Sinopoulos, P., ‘Functional equations on semigroups’, Aequationes Math. 59 (2000), 255–261.CrossRefGoogle Scholar
Stetkær, H., ‘Functional equations on abelian groups with involution’, Aequationes Math. 54 (1997), 144–172.Google Scholar
Stetkær, H., ‘Functional equations on abelian groups with involution II’, Aequationes Math. 55 (1998), 227–240.Google Scholar
Szabo, Gy., ‘Some functional equations related to quadratic functions’, Glas. Mat. 38 (1983), 107–118.Google Scholar
Székelyhidi, L., Convolution Type Functional Equations on Topological Abelian Groups (World Scientific, Singapore, 1991).Google Scholar
Zhang, D., ‘On hyperstability of generalised linear functional equations in several variables’, Bull. Aust. Math. Soc. 92 (2015), 259–267.Google Scholar