Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T05:01:25.818Z Has data issue: false hasContentIssue false
  • English
  • Français

On the inversion of Fourier transforms

Published online by Cambridge University Press:  17 April 2009

Nakhlé H. Asmar  and
Kent G. Merryfield
Nakhlé H. Asmar
Affiliation:
Department of MathematicsUniversity of Missouri, ColumbiaColumbia, MO 65211United States of America
Kent G. Merryfield
Affiliation:
Department of MathematicsCalifornia State University, Long BeachLong Beach, CA 90840United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact abelian group, with character group Ĝ. Let ψ be an arbitrary continuous real-valued homomorphism defined on Ĝ. For f in LP(G), 1 < p ≤ 2, let

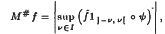
where 1[−ν, ν] is the indicator function of the interval [ − ν, ν ], and I is an unbounded increasing sequence of positive real numbers. Then there is a constant Mp, independent of f, such that ‖M#f‖p ≤ Mp ‖f‖p. Consequently, the pointwise limit of the function 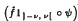exists, almost everywhere on G, as ν tends to infinity. Using this result and a generalised version of Riesz's theorem on conjugate functions, we obtain a pointwise inversion for Fourier transforms of functions on Ra × Tb, where a and b are nonnegative integers, and on various other locally compact abelian groups.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 40 , Issue 3 , December 1989 , pp. 429 - 439
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Asmar, N. and Hewitt, B., Marcel Riesz's theorem on conjugate Fourier series and its descendants: Proc. of theAnalysis Conference Singapore (North Holland, Amsterdam, 1988).Google Scholar
[2]Asmar, N., Berkson, E. and Gillespie, T.A., ‘Representations of groups with ordered duals and generalized analyticity’, J. Funct. Anal. (to appear).Google Scholar
[3]Calderón, A.P., ‘Ergodic theory and translation-invariant operators’, Proc. Nat. Acad. Sci. U.S.A. 59 (1968), 349–353.CrossRefGoogle ScholarPubMed
[4]Coifman, R.R. and Weiss, G., Transference methods in analysis 31, Conference Board of the Mathematical Sciences; Regional Conference Series in Mathematics (American Mathematical Society,Providence, 1977).CrossRefGoogle Scholar
[5]Fefferman, C., ‘On the convergence of multiple Fourier series’, Bull. Amer. Math. Soc. 77 (1971), 744–745.CrossRefGoogle Scholar
[6]Fefferman, C., ‘On the divergence of multiple Fourier series’, Bull. Amer. Math. Soc. 77 (1971), 191–195.CrossRefGoogle Scholar
[7]De Guzmán, M., Real variable methods in Fourier analysis, North-Holland Mathematics Studies No. 46 (North Holland Publishing Co, Amsterdam, 1981).Google Scholar
[8]Hewitt, E. and Ross, K.A., Abstract harmonic analysis, Vo. 1, (2nd Edition, Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
[9]Hewitt, E. and Ross, K.A., Abstract harmonic analysis, Vol 2 (Springer-Verlag, Berlin, 1970).Google Scholar
[10]Kenig, C.E. and Tomas, P.A., ‘Maximal operators defined by Fourier multipliers’, Studia Math 68 (1980), 79–83.CrossRefGoogle Scholar
[11]Zygmund, A., Trigonometric series, Vol 1 and 2 (2nd rev. ed., Cambridge Univ. Press, New York, 1959).Google Scholar