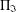Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T13:58:18.437Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LATTICE OF $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-SUBNORMAL SUBGROUPS OF A FINITE GROUP

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  02 May 2017

WENBIN GUO  and
ALEXANDER N. SKIBA
WENBIN GUO*
Affiliation:
Department of Mathematics, University of Science and Technology of China, Hefei 230026, PR China email wbguo@ustc.edu.cn
ALEXANDER N. SKIBA
Affiliation:
Department of Mathematics, Francisk Skorina Gomel State University, Gomel 246019, Belarus email alexander.skiba49@gmail.com
*
✉wbguo@ustc.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 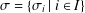$\unicode[STIX]{x1D70E}=\{\unicode[STIX]{x1D70E}_{i}\mid i\in I\}$ be a partition of the set of all primes $\mathbb{P}$. Let 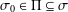$\unicode[STIX]{x1D70E}_{0}\in \unicode[STIX]{x1D6F1}\subseteq \unicode[STIX]{x1D70E}$ and let 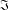$\mathfrak{I}$ be a class of finite 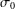$\unicode[STIX]{x1D70E}_{0}$-groups which is closed under extensions, epimorphic images and subgroups. 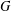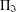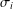We say that a finite group $G$ is $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-primary provided $G$ is either an $\mathfrak{I}$-group or a $\unicode[STIX]{x1D70E}_{i}$-group for some 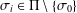$\unicode[STIX]{x1D70E}_{i}\in \unicode[STIX]{x1D6F1}\setminus \{\unicode[STIX]{x1D70E}_{0}\}$ and we say that a subgroup 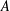$A$ of an arbitrary group 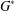$G^{\ast }$ is 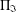$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-subnormal in 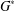$G^{\ast }$ if there is a subgroup chain 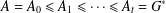$A=A_{0}\leq A_{1}\leq \cdots \leq A_{t}=G^{\ast }$ such that either 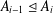$A_{i-1}\unlhd A_{i}$ or 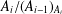$A_{i}/(A_{i-1})_{A_{i}}$ is 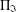$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-primary for all $i=1,\ldots ,t$. We prove that the set 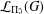${\mathcal{L}}_{\unicode[STIX]{x1D6F1}_{\mathfrak{I}}}(G)$ of all $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-subnormal subgroups of 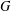$G$ forms a sublattice of the lattice of all subgroups of 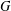$G$ and we describe the conditions under which the lattice 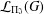${\mathcal{L}}_{\unicode[STIX]{x1D6F1}_{\mathfrak{I}}}(G)$ is modular.

Keywords

finite group𝛱ℑ -subnormal subgroup𝛱ℑ -nilpotent grouplatticemodular lattice

MSC classification

Primary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D30: Series and lattices of subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 233 - 244
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The research is supported by NNSF of China (grant no. 11371335) and the Wu Wen-Tsun Key Laboratory of Mathematics of the Chinese Academy of Sciences.

References

Al-Sharo, K. A. and Skiba, A. N., ‘On finite groups with 𝜎-subnormal Schmidt subgroups’, Comm. Algebra. to appear. Published online (21 October 2016).Google Scholar
Ballester-Bolinches, A., Doerk, K. and Pèrez-Ramos, M. D., ‘On the lattice of F-subnormal subgroups’, J. Algebra 148 (1992), 42–52.CrossRefGoogle Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups (Springer, Dordrecht, 2006).Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (Walter de Gruyter, Berlin, 1992).CrossRefGoogle Scholar
Grätzer, G., General Lattice Theory (Birkhäuser, Basel–Stuttgart, 1978).CrossRefGoogle Scholar
Guo, W. and Skiba, A. N., ‘Finite groups with permutable complete Wielandt sets of subgroups’, J. Group Theory 18 (2014), 191–200.CrossRefGoogle Scholar
Guo, W. and Skiba, A. N., ‘Finite groups whose $n$ -maximal subgroups are $\unicode[STIX]{x1D70E}$ -subnormal’, arXiv:1608.03353 [math.GR].Google Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin–Heidelberg–New York, 1967).CrossRefGoogle Scholar
Kegel, O. H., ‘Untergruppenverbande endlicher Gruppen, die den Subnormalteilerverband echt enthalten’, Arch. Math. 30(3) (1978), 225–228.CrossRefGoogle Scholar
Schmidt, R., Subgroup Lattices of Groups (Walter de Gruyter, Berlin, 1994).CrossRefGoogle Scholar
Shemetkov, L. A., Formations of Finite Groups (Nauka, Main Editorial Board for Physical and Mathematical Literature, Moscow, 1978).Google Scholar
Skiba, A. N., ‘A generalization of a Hall theorem’, J. Algebra Appl. 15(4) (2015), 21–36.Google Scholar
Skiba, A. N., ‘On 𝜎-subnormal and 𝜎-permutable subgroups of finite groups’, J. Algebra 436 (2015), 1–16.CrossRefGoogle Scholar
Vasil’ev, A. F., Kamornikov, A. F. and Semenchuk, V. N., ‘On lattices of subgroups of finite groups’, in: Infinite Groups and Related Algebraic Structures (ed. Chernikov, N. S.) (Institum Matemayiki AN Ukrainy, Kiev, 1993), 27–54 (in Russian).Google Scholar
Zappa, G., ‘Sui gruppi finiti per cui il reticolo dei sottogruppi di composizione e modulare’, Boll. Unione Mat. Ital. 11(3) (1956), 315–318.Google Scholar