Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T06:10:44.851Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE MINIMAL NUMBER OF SMALL ELEMENTS GENERATING FINITE PRIME FIELDS

Part of: Multiplicative number theory Elementary number theory

Published online by Cambridge University Press:  17 August 2017

MARC MUNSCH
MARC MUNSCH*
Affiliation:
5010 Institut für Analysis und Zahlentheorie, 8010 Graz, Steyrergasse 30, Graz, Austria email munsch@math.tugraz.at
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, we give an upper bound for the number of elements from the interval 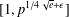$[1,p^{1/4\sqrt{e}+\unicode[STIX]{x1D716}}]$ necessary to generate the finite field 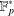$\mathbb{F}_{p}^{\ast }$ with 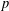$p$ an odd prime. The general result depends on the distribution of the divisors of 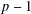$p-1$ and can be used to deduce results which hold for almost all primes.

Keywords

finite fieldgenerating setprimitive rootsieve theorycharacter sumalgorithmic number theory

MSC classification

Primary: 11A07: Congruences; primitive roots; residue systems
Secondary: 11N36: Applications of sieve methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 177 - 184
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Ankeny, N. C., ‘The least quadratic non residue’, Ann. of Math. (2) 55 (1952), 65–72.CrossRefGoogle Scholar
Bombieri, E., ‘On the large sieve’, Mathematika 12 (1965), 201–225.CrossRefGoogle Scholar
Burgess, D. A., ‘On character sums and primitive roots’, Proc. Lond. Math. Soc. (3) 12 (1962), 179–192.CrossRefGoogle Scholar
Burgess, D. A. and Elliott, P. D. T. A., ‘The average of the least primitive root’, Mathematika 15 (1968), 39–50.CrossRefGoogle Scholar
Burthe, R. J. Jr, ‘Upper bounds for least witnesses and generating sets’, Acta Arith. 80(4) (1997), 311–326.CrossRefGoogle Scholar
Granville, A., Koukoulopoulos, D. and Matomäki, K., ‘When the sieve works’, Duke Math. J. 164(10) (2015), 1935–1969.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., ‘Sieving and the Erdös–Kac theorem’, in: Equidistribution in Number Theory, an Introduction, NATO Science Series II: Mathematics, Physics and Chemistry, 237 (Springer, Dordrecht, 2007), 15–27.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 6th edn (Oxford University Press, Oxford, 2008), Revised by D. R. Heath-Brown and J. H. Silverman.CrossRefGoogle Scholar
Harman, G. and Shparlinski, I. E., ‘Products of small integers in residue classes and additive properties of Fermat quotients’, Int. Math. Res. Not. IMRN 2016(5) (2016), 1424–1446.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Artin’s conjecture for primitive roots’, Quart. J. Math. Oxford Ser. (2) 37(145) (1986), 27–38.CrossRefGoogle Scholar
Hooley, C., ‘On Artin’s conjecture’, J. reine angew. Math. 225 (1967), 209–220.Google Scholar
Matomäki, K. and Shao, X., ‘When the sieve works ii’. Preprint, 2015, arXiv:1509.02371.Google Scholar
Moree, P., ‘Artin’s primitive root conjecture—a survey’, Integers 12(6) (2012), 1305–1416.CrossRefGoogle Scholar
Pappalardi, F., ‘On minimal sets of generators for primitive roots’, Canad. Math. Bull. 38(4) (1995), 465–468.CrossRefGoogle Scholar
Shoup, V., ‘Searching for primitive roots in finite fields’, Math. Comp. 58(197) (1992), 369–380.CrossRefGoogle Scholar
Turán, P., ‘On a theorem of Hardy and Ramanujan’, J. Lond. Math. Soc. S1‐9(4) (1934), 274–276.CrossRefGoogle Scholar
Vinogradov, J. M., ‘On a general theorem concerning the distribution of the residues and non-residues of powers’, Trans. Amer. Math. Soc. 29(1) (1927), 209–217.CrossRefGoogle Scholar
Vinogradov, J. M., ‘On the bound of the least non-residue of nth powers’, Trans. Amer. Math. Soc. 29(1) (1927), 218–226.Google Scholar