Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T10:11:10.788Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PERIODICITY OF TRANSCENDENTAL ENTIRE FUNCTIONS

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  13 February 2020

XINLING LIU Open the ORCID record for XINLING LIU [Opens in a new window]  and
RISTO KORHONEN Open the ORCID record for RISTO KORHONEN [Opens in a new window]
XINLING LIU
Affiliation:
Department of Mathematics,Nanchang University, Nanchang, Jiangxi, 330031, PR China Department of Physics and Mathematics,University of Eastern Finland, PO Box 111, 80101, Joensuu, Finland email liuxinling@ncu.edu.cn
RISTO KORHONEN*
Affiliation:
Department of Physics and Mathematics,University of Eastern Finland, PO Box 111, 80101, Joensuu, Finland email risto.korhonen@uef.fi
*
✉risto.korhonen@uef.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

According to a conjecture by Yang, if 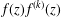$f(z)f^{(k)}(z)$ is a periodic function, where 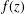$f(z)$ is a transcendental entire function and 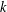$k$ is a positive integer, then 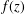$f(z)$ is also a periodic function. We propose related questions, which can be viewed as difference or differential-difference versions of Yang’s conjecture. We consider the periodicity of a transcendental entire function 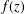$f(z)$ when differential, difference or differential-difference polynomials in 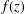$f(z)$ are periodic. For instance, we show that if 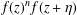$f(z)^{n}f(z+\unicode[STIX]{x1D702})$ is a periodic function with period $c$, then 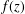$f(z)$ is also a periodic function with period 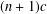$(n+1)c$, where 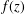$f(z)$ is a transcendental entire function of hyper-order 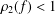$\unicode[STIX]{x1D70C}_{2}(f)<1$ and 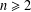$n\geq 2$ is an integer.

Keywords

entire functionsperiodicitygrowth

MSC classification

Primary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 453 - 465
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by the NSFC (No. 11661052) and EDUFI Fellowship No. 18-11020. The second author was partially supported by the Academy of Finland Grant No. 286877.

References

Baker, I. N., ‘On some results of A. Rényi and C. Rényi concerning periodic entire functions’, Acta Sci. Math. (Szeged) 27 (1966), 197–200.Google Scholar
Chen, W., Hu, P. C. and Zhang, Y. Y., ‘On solutions to some nonlinear difference and differential equations’, J. Korean Math. Soc. 53(4) (2016), 835–846.10.4134/JKMS.j150296CrossRefGoogle Scholar
Chuang, C. T. and Yang, C. C., Fix-Points and Factorization of Meromorphic Functions (World Scientific, Singapore, 1990).Google Scholar
Gross, F., ‘On the equation f n + g n = h n’, Amer. Math. Monthly 73 (1966), 1093–1096.CrossRefGoogle Scholar
Gross, F. and Yang, C. C., ‘On periodic entire functions’, Rend. Circ. Mat. Palermo 21(3) (1972), 284–292.10.1007/BF02843792CrossRefGoogle Scholar
Halász, G., ‘On the periodicity of composed integral functions’, Period. Math. Hungar. 2 (1972), 73–83.10.1007/BF02018653CrossRefGoogle Scholar
Halburd, R. G., Korhonen, R. J. and Tohge, K., ‘Holomorphic curves with shift-invariant hyperplane preimages’, Trans. Amer. Math. Soc. 366 (2014), 4267–4298.CrossRefGoogle Scholar
Hayman, W. K., Meromorphic Functions (Clarendon Press, Oxford, 1964).Google Scholar
Heittokangas, J., Korhonen, R., Laine, I., Rieppo, J. and Zhang, J. L., ‘Value sharing results for shifts of meromorphic functions, and sufficient conditions for periodicity’, Math. Anal. Appl. 355 (2009), 352–363.CrossRefGoogle Scholar
Laine, I., Nevanlinna Theory and Complex Differential Equations (Walter de Gruyter, Berlin–New York, 1993).10.1515/9783110863147CrossRefGoogle Scholar
Liu, K., Cao, T. B. and Cao, H. Z., ‘Entire solutions of Fermat type differential-difference equations’, Arch. Math. 99 (2012), 147–155.CrossRefGoogle Scholar
Liu, K., Liu, X. L. and Yang, L. Z., ‘The zero distribution and uniqueness of difference-differential polynomials’, Ann. Polon. Math. 109 (2013), 137–152.10.4064/ap109-2-3CrossRefGoogle Scholar
Liu, K. and Yu, P. Y., ‘A note on the periodicity of entire functions’, Bull. Aust. Math. Soc. 100(2) (2019), 290–296.10.1017/S0004972719000030CrossRefGoogle Scholar
Ozawa, M., ‘On the existence of prime periodic entire functions’, Kodai Math. Sem. Rep. 29 (1978), 308–321.10.2996/kmj/1138833654CrossRefGoogle Scholar
Rényi, A. and Rényi, C., ‘Some remarks on periodic entire functions’, J. Anal. Math. 14(1) (1965), 303–310.10.1007/BF02806397CrossRefGoogle Scholar
Wang, Q. and Hu, P. C., ‘On zeros and periodicity of entire functions’, Acta Math. Sci. 38A(2) (2018), 209–214.Google Scholar
Yang, C. C., ‘A generalization of a theorem of P. Montel on entire functions’, Proc. Amer. Math. Soc. 26 (1970), 332–334.10.1090/S0002-9939-1970-0264080-XCrossRefGoogle Scholar
Yang, C. C., ‘On periodicity of entire functions’, Proc. Amer. Math. Soc. 43 (1974), 353–356.CrossRefGoogle Scholar
Yang, C. C. and Yi, H. X., Uniqueness Theory of Meromorphic Functions (Springer, Dordrecht, 2003).10.1007/978-94-017-3626-8CrossRefGoogle Scholar