Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T03:20:08.254Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PRONORM OF A GROUP

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  20 January 2021

MATTIA BRESCIA Open the ORCID record for MATTIA BRESCIA [Opens in a new window]  and
ALESSIO RUSSO Open the ORCID record for ALESSIO RUSSO [Opens in a new window]
MATTIA BRESCIA
Affiliation:
Dipartimento di Matematica e Applicazioni, Università degli Studi di Napoli Federico II, Corso Umberto I, 40, Napoli, Italy e-mail: mattia.brescia@unina.it
ALESSIO RUSSO*
Affiliation:
Dipartimento di Matematica e Fisica, Università degli Studi della Campania ‘Luigi Vanvitelli’, Viale Lincoln 5, Caserta, Italy
*
e-mail: alessio.russo@unicampania.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The pronorm of a group G is the set 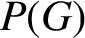$P(G)$ of all elements 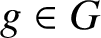$g\in G$ such that X and 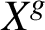$X^g$ are conjugate in 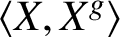${\langle {X,X^g}\rangle }$ for every subgroup X of G. In general the pronorm is not a subgroup, but we give evidence of some classes of groups in which this property holds. We also investigate the structure of a generalised soluble group G whose pronorm contains a subgroup of finite index.

Keywords

pronormal subgrouppronorm of a groupT-group

MSC classification

Primary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Secondary: 20F19: Generalizations of solvable and nilpotent groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 287 - 294
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are members of GNSAGA-INdAM and ADV-AGTA. This work was carried out within the ‘VALERE: VAnviteLli pEr la RicErca’ project.

References

Baer, R., ‘Der Kern, eine charakteristische Untergruppe’, Compos. Math. 1 (1934), 254–283.Google Scholar
Brescia, M. and Russo, A., ‘On cyclic automorphisms of a group’, J. Algebra Appl., to appear.Google Scholar
de Giovanni, F., Russo, A. and Vincenzi, G., ‘Groups in which every subgroup is almost pronormal’, Note Mat. 1 (2008), 95–103.Google Scholar
de Giovanni, F. and Vincenzi, G., ‘Pronormality in infinite groups’, Proc. Roy. Irish Acad. 200A (2000), 189–203.Google Scholar
de Giovanni, F. and Vincenzi, G., ‘Some topics in the theory of pronormal subgroups of groups’, Quad. Mat. 8 (2001), 175–202.Google Scholar
Dixon, M. R., Sylow Theory, Formations and Fitting Classes in Locally Finite Groups (World Scientific Publishing, Singapore, 1994).CrossRefGoogle Scholar
Gaschütz, W., ‘Gruppen, in denen das Normalteilersein transitiv ist’, J. reine angew. Math. 198 (1957), 87–92.Google Scholar
Khukhro, E. I. and Mazurov, V. D., Kourova Notebook, Vol. 16 (Russian Academy of Sciences, Novosibirsk, 2006).Google Scholar
Kuzennyi, N. F. and Subbotin, I. Y., ‘Groups in which all subgroups are pronormal’, Ukrainian Math. J. 39 (1987), 251–254.CrossRefGoogle Scholar
Neumann, B. H., ‘Groups with finite classes of conjugate subgroups’, Math. Z. 63 (1955), 76–96.CrossRefGoogle Scholar
Peng, T. A., ‘Finite groups with pro-normal subgroups’, Proc. Amer. Math. Soc. 20 (1969), 232–234.CrossRefGoogle Scholar
Robinson, D. J. S., ‘Groups in which normality is a transitive relation’, Proc. Cambridge Philos. Soc. 60 (1964), 21–38.CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer-Verlag, Berlin, 1972).CrossRefGoogle Scholar
Robinson, D. J. S., Russo, A. and Vincenzi, G., ‘On groups which contain no HNN-extension’, Internat. J. Algebra Comput. 17 (2005), 1377–1387.CrossRefGoogle Scholar
Rose, J. S., ‘Finite soluble groups with pronormal system normalizers’, Proc. Lond. Math. Soc. 17 (1967), 447–469.CrossRefGoogle Scholar
Russo, A., ‘On groups in which normality is a transitive relation’, Comm. Algebra 40 (2012), 3950–3954.CrossRefGoogle Scholar