Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T03:56:54.478Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SELMER GROUP OF A CERTAIN 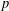$p$-ADIC LIE EXTENSION

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  27 February 2019

AMALA BHAVE Open the ORCID record for AMALA BHAVE [Opens in a new window]  and
LACHIT BORA Open the ORCID record for LACHIT BORA [Opens in a new window]
AMALA BHAVE*
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi, India-110067 email amalasarma@gmail.com
LACHIT BORA
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi, India-110067 email boralachit3@gmail.com
*
✉amalasarma@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 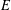$E$ be an elliptic curve over 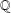$\mathbb{Q}$ without complex multiplication. Let 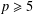$p\geq 5$ be a prime in 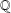$\mathbb{Q}$ and suppose that 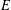$E$ has good ordinary reduction at 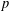$p$. We study the dual Selmer group of 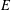$E$ over the compositum of the 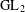$\text{GL}_{2}$ extension and the anticyclotomic 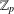$\mathbb{Z}_{p}$-extension of an imaginary quadratic extension as an Iwasawa module.

Keywords

elliptic curveanticyclotomic extensionGalois groupIwasawa moduleSelmer group

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11R20: Other abelian and metabelian extensions 11R34: Galois cohomology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 245 - 255
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author acknowledges the support of DST PURSE and UPE II grants; the second author is supported by a UGC-BSR fellowship.

References

Balister, P. N. and Howson, S., ‘Note on Nakayama’s lemma for compact 𝛬-modules’, Asian. J. Math. 1(2) (1997), 224–229.10.4310/AJM.1997.v1.n2.a2Google Scholar
Bhave, A., ‘Analogue of Kida’s formula for certain strongly admissible extensions’, J. Number Theory 122 (2007), 100–120.10.1016/j.jnt.2006.02.008Google Scholar
Coates, J. H. and Howson, S., ‘Euler characteristics and elliptic curves II’, J. Math. Soc. Japan 53(1) (2001), 175–235.10.2969/jmsj/05310175Google Scholar
Coates, J. H. and Sujatha, R., Galois Cohomology of Elliptic Curves, Tata Institute of Fundamental Research, Lectures on Mathematics, 88 (Narosa Publishing House, New Delhi, 2000).Google Scholar
Greenberg, R., ‘Iwasawa theory for elliptic curves’, in: Arithmetic Theory of Elliptic Curves, Lecture Notes in Mathematics, 1716 (ed. Viola, C.) (Springer, Berlin–Heidelberg, 1999), 51–144.10.1007/BFb0093453Google Scholar
Imai, H., ‘A remark on the rational points of Abelian varieties with values in cyclotomic ℤp-extensions’, Proc. Japan. Acad. Math. Sci. 51 (1975), 12–16.Google Scholar
Lazard, M., ‘Groupes analytiques p-adiques’, Publ. Inst. Hautes Études Sci. 26 (1965), 389–603.Google Scholar
Mazur, B., ‘Rational points of abelian varieties with values in towers of number fields’, Invent. Math. 18 (1972), 183–266.10.1007/BF01389815Google Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15 (1972), 259–331.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 106 (Springer, New York, 2009).10.1007/978-0-387-09494-6Google Scholar
Washington, L. C., Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, 83 (Springer, New York, 1982).Google Scholar