Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T22:13:48.340Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE STRONG METRIC DIMENSION OF A TOTAL GRAPH OF NONZERO ANNIHILATING IDEALS

Part of: General commutative ring theory Graph theory Ring extensions and related topics

Published online by Cambridge University Press:  04 November 2021

N. ABACHI Open the ORCID record for N. ABACHI [Opens in a new window] ,
M. ADLIFARD Open the ORCID record for M. ADLIFARD [Opens in a new window]  and
M. BAKHTYIARI Open the ORCID record for M. BAKHTYIARI [Opens in a new window]
N. ABACHI
Affiliation:
Department of Mathematics, Buinzahra Branch, Islamic Azad University, Buinzahra, Iran e-mail: n_abachi@yahoo.com
M. ADLIFARD
Affiliation:
Department of Mathematics, Roudbar Branch, Islamic Azad University, Roudbar, Iran e-mail: m.adlifard@iauroudbar.ac.ir
M. BAKHTYIARI*
Affiliation:
Faculty of Mathematics, K. N. Toosi University of Technology, P.O. Box 16315-1618, Tehran, Iran
*
e-mail: m.bakhtyiari55@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a commutative ring with identity which is not an integral domain. An ideal I of R is called an annihilating ideal if there exists 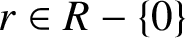$r\in R- \{0\}$ such that 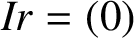$Ir=(0)$ . The total graph of nonzero annihilating ideals of R is the graph 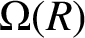$\Omega (R)$ whose vertices are the nonzero annihilating ideals of R and two distinct vertices 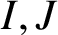$I,J$ are joined if and only if 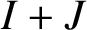$I+J$ is also an annihilating ideal of R. We study the strong metric dimension of 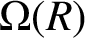$\Omega (R)$ and evaluate it in several cases.

Keywords

strong metric dimensionmaximally distantannihilating idealresolving set

MSC classification

Primary: 13A15: Ideals; multiplicative ideal theory
Secondary: 05C99: None of the above, but in this section 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 13B99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 431 - 439
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abachi, N. and Sahebi, S., ‘On the metric dimension of a total graph of non-zero annihilating ideals’, An. Ştiinţ. Univ. “Ovidius” Constanţa Ser. Mat. 28(3) (2020), 5–14.Google Scholar
Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Chartrand, G., Eroh, L., Johnson, M. A. and Oellermann, O. R., ‘Resolvability in graphs and the metric dimension of a graph’, Discrete Appl. Math. 105 (2000), 99–113.CrossRefGoogle Scholar
Dolžan, D., ‘The metric dimension of the total graph of a finite commutative ring’, Canad. Math. Bull. 59 (2016), 748–759.CrossRefGoogle Scholar
Dolžan, D., ‘The metric dimension of the annihilating-ideal graph of a finite commutative ring’, Bull. Aust. Math. Soc. 103(3) (2021), 362–368.CrossRefGoogle Scholar
Harary, F. and Melter, R. A., ‘On the metric dimension of a graph’, Ars Combin. 2 (1976), 191–195.Google Scholar
Khuller, S., Raghavachari, B. and Rosenfeld, A., ‘Landmarks in graphs’, Discrete Appl. Math. 70(3) (1996), 217–229.Google Scholar
Kuziak, D., Yero, I. G. and Rodríguez-Velázquez, J. A., ‘On the strong metric dimension of the strong products of graphs’, Open Math. 13 (2015), 64–74.Google Scholar
May, T. R. and Oellermann, O. R., ‘The strong metric dimension of distance hereditary graphs’, J. Combin. Math. Combin. Comput. 76(3) (2011), 59–73.Google Scholar
Oellermann, O. R. and Peters-Fransen, J., ‘The strong metric dimension of graphs and digraphs’, Discrete Appl. Math. 155 (2007), 356–364.Google Scholar
Pirzada, S. and Aijaz, M., ‘Metric and upper dimension of zero divisor graphs associated to commutative rings’, Acta Univ. Sapientiae Inform. 12(1) (2020), 84–101.CrossRefGoogle Scholar
Pirzada, S. and Imran Bhat, M., ‘Computing metric dimension of compressed zero divisor graphs associated to rings’, Acta Univ. Sapientiae Math. 10(2) (2018), 298–318.Google Scholar
Pirzada, S. and Raja, R., ‘On the metric dimension of a zero-divisor graph’, Comm. Algebra 45(4) (2017), 1399–1408.CrossRefGoogle Scholar
Shanmukha, B., Sooryanarayana, B. and Harinath, K., ‘Metric dimension of wheels’, Far East J. Appl. Math. 8(3) (2002), 217–229.Google Scholar
Visweswaran, S. and Patel, H. D., ‘A graph associated with the set of all nonzero annihilating ideals of a commutative ring’, Discrete Math. Algorithms Appl. 6(4) (2014), Article no. 1450047, 22 pages.CrossRefGoogle Scholar
West, D. B., Introduction to Graph Theory, 2nd edn (Prentice Hall, Upper Saddle River, NJ, 2001).Google Scholar