No CrossRef data available.
Article contents
ON THE TWO-PARAMETER ERDŐS–FALCONER DISTANCE PROBLEM IN FINITE FIELDS
Published online by Cambridge University Press: 29 September 2022
Abstract
Given
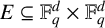 $E \subseteq \mathbb {F}_q^d \times \mathbb {F}_q^d$
, with the finite field
$E \subseteq \mathbb {F}_q^d \times \mathbb {F}_q^d$
, with the finite field
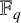 $\mathbb {F}_q$
of order q and the integer
$\mathbb {F}_q$
of order q and the integer
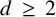 $d\,\ge \, 2$
, we define the two-parameter distance set
$d\,\ge \, 2$
, we define the two-parameter distance set
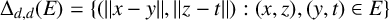 $\Delta _{d, d}(E)=\{(\|x-y\|, \|z-t\|) : (x, z), (y, t) \in E \}$
. Birklbauer and Iosevich [‘A two-parameter finite field Erdős–Falconer distance problem’, Bull. Hellenic Math. Soc. 61 (2017), 21–30] proved that if
$\Delta _{d, d}(E)=\{(\|x-y\|, \|z-t\|) : (x, z), (y, t) \in E \}$
. Birklbauer and Iosevich [‘A two-parameter finite field Erdős–Falconer distance problem’, Bull. Hellenic Math. Soc. 61 (2017), 21–30] proved that if
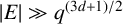 $|E| \gg q^{{(3d+1)}/{2}}$
, then
$|E| \gg q^{{(3d+1)}/{2}}$
, then
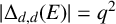 $ |\Delta _{d, d}(E)| = q^2$
. For
$ |\Delta _{d, d}(E)| = q^2$
. For
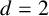 $d=2$
, they showed that if
$d=2$
, they showed that if
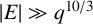 $|E| \gg q^{{10}/{3}}$
, then
$|E| \gg q^{{10}/{3}}$
, then
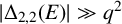 $ |\Delta _{2, 2}(E)| \gg q^2$
. In this paper, we give extensions and improvements of these results. Given the diagonal polynomial
$ |\Delta _{2, 2}(E)| \gg q^2$
. In this paper, we give extensions and improvements of these results. Given the diagonal polynomial
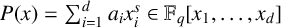 $P(x)=\sum _{i=1}^da_ix_i^s\in \mathbb F_q[x_1,\ldots , x_d]$
, the distance induced by P over
$P(x)=\sum _{i=1}^da_ix_i^s\in \mathbb F_q[x_1,\ldots , x_d]$
, the distance induced by P over
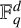 $\mathbb {F}_q^d$
is
$\mathbb {F}_q^d$
is
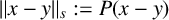 $\|x-y\|_s:=P(x-y)$
, with the corresponding distance set
$\|x-y\|_s:=P(x-y)$
, with the corresponding distance set
 $\Delta ^s_{d, d}(E)=\{(\|x-y\|_s, \|z-t\|_s) : (x, z), (y, t) \in E \}$
. We show that if
$\Delta ^s_{d, d}(E)=\{(\|x-y\|_s, \|z-t\|_s) : (x, z), (y, t) \in E \}$
. We show that if
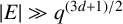 $|E| \gg q^{{(3d+1)}/{2}}$
, then
$|E| \gg q^{{(3d+1)}/{2}}$
, then
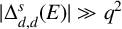 $ |\Delta _{d, d}^s(E)| \gg q^2$
. For
$ |\Delta _{d, d}^s(E)| \gg q^2$
. For
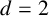 $d=2$
and the Euclidean distance, we improve the former result over prime fields by showing that
$d=2$
and the Euclidean distance, we improve the former result over prime fields by showing that
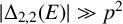 $ |\Delta _{2,2}(E)| \gg p^2$
for
$ |\Delta _{2,2}(E)| \gg p^2$
for
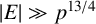 $|E| \gg p^{{13}/{4}}$
.
$|E| \gg p^{{13}/{4}}$
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The second-listed author was supported by Swiss National Science Foundation grant P2ELP2-178313.



