Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:59:53.926Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 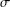$\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  12 November 2018

BIN HU ,
JIANHONG HUANG Open the ORCID record for JIANHONG HUANG [Opens in a new window]  and
ALEXANDER N. SKIBA
BIN HU
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China email hubin118@126.com
JIANHONG HUANG*
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China email jhh320@126.com
ALEXANDER N. SKIBA
Affiliation:
Department of Mathematics and Technologies of Programming, Francisk Skorina Gomel State University, Gomel 246019, Belarus email alexander.skiba49@gmail.com
*
✉jhh320@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 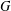$G$ be a finite group and 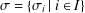$\unicode[STIX]{x1D70E}=\{\unicode[STIX]{x1D70E}_{i}\mid i\in I\}$ some partition of the set of all primes 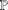$\mathbb{P}$, that is, 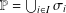$\mathbb{P}=\bigcup _{i\in I}\unicode[STIX]{x1D70E}_{i}$ and 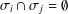$\unicode[STIX]{x1D70E}_{i}\cap \unicode[STIX]{x1D70E}_{j}=\emptyset$ for all 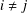$i\neq j$. We say that 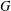$G$ is 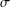$\unicode[STIX]{x1D70E}$-primary if 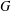$G$ is a 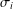$\unicode[STIX]{x1D70E}_{i}$-group for some 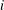$i$. A subgroup 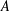$A$ of 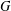$G$ is said to be: 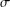$\unicode[STIX]{x1D70E}$-subnormal in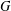$G$ if there is a subgroup chain 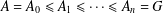$A=A_{0}\leq A_{1}\leq \cdots \leq A_{n}=G$ such that either 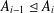$A_{i-1}\unlhd A_{i}$ or 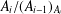$A_{i}/(A_{i-1})_{A_{i}}$ is 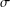$\unicode[STIX]{x1D70E}$-primary for all 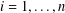$i=1,\ldots ,n$; modular in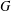$G$ if the following conditions hold: (i) 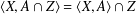$\langle X,A\cap Z\rangle =\langle X,A\rangle \cap Z$ for all 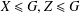$X\leq G,Z\leq G$ such that 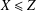$X\leq Z$ and (ii) 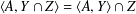$\langle A,Y\cap Z\rangle =\langle A,Y\rangle \cap Z$ for all 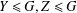$Y\leq G,Z\leq G$ such that 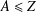$A\leq Z$; and 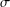$\unicode[STIX]{x1D70E}$-quasinormal in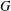$G$ if 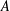$A$ is modular and 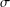$\unicode[STIX]{x1D70E}$-subnormal in 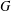$G$. We study 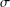$\unicode[STIX]{x1D70E}$-quasinormal subgroups of 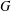$G$. In particular, we prove that if a subgroup 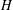$H$ of 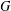$G$ is 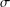$\unicode[STIX]{x1D70E}$-quasinormal in 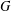$G$, then every chief factor 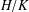$H/K$ of 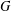$G$ between 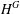$H^{G}$ and 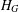$H_{G}$ is 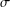$\unicode[STIX]{x1D70E}$-central in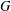$G$, that is, the semidirect product 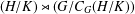$(H/K)\rtimes (G/C_{G}(H/K))$ is 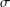$\unicode[STIX]{x1D70E}$-primary.

Keywords

finite group𝜎-nilpotent group𝜎-subnormal subgroupmodular subgroup𝜎-quasinormal subgroup

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D15: Nilpotent groups, $p$-groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 413 - 420
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

Research is supported by an NNSF grant of China (Grant No. 11401264) and a TAPP of Jiangsu Higher Education Institutions (PPZY 2015A013).

References

Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups (Walter de Gruyter, Berlin–New York, 2010).Google Scholar
Chunikhin, S. A., Subgroups of Finite Groups (Nauka i Tehnika, Minsk, 1964).Google Scholar
Guo, W. and Skiba, A. N., ‘Finite groups whose n-maximal subgroups are 𝜎-subnormal’, Sci. China Math. 62; doi:10.1007/s11425-016-9211-9.Google Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin–Heidelberg, 1967).Google Scholar
Ito, N. and Szép, J., ‘Uber die Quasinormalteiler von endlichen Gruppen’, Acta Sci. Math. 23 (1962), 168–170.Google Scholar
Kegel, O. H., ‘Untergruppenverbande endlicher Gruppen, die den Subnormalteilerverband echt enthalten’, Arch. Math. 30(3) (1978), 225–228.Google Scholar
Maier, R. and Schmid, P., ‘The embedding of permutable subgroups in finite groups’, Math. Z. 131 (1973), 269–272.Google Scholar
Ore, O., ‘Contributions in the theory of groups of finite order’, Duke Math. J. 5 (1939), 431–460.Google Scholar
Schmidt, R., Subgroup Lattices of Groups (Walter de Gruyter, Berlin, 1994).Google Scholar
Skiba, A. N., ‘On 𝜎-subnormal and 𝜎-permutable subgroups of finite groups’, J. Algebra 436 (2015), 1–16.Google Scholar
Skiba, A. N., ‘Some characterizations of finite 𝜎-soluble P𝜎T-groups’, J. Algebra 495 (2018), 114–129.Google Scholar
Thompson, J. G., ‘An example of core-free quasinormal subgroup of p-group’, Math. Z. 96 (1973), 226–227.Google Scholar