Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T01:56:26.747Z Has data issue: false hasContentIssue false
  • English
  • Français

On vector spaces of certain modular forms of given weights: Addendum

Published online by Cambridge University Press:  17 April 2009

A.R. Aggarwal  and
M.K. Agrawal
A.R. Aggarwal
Affiliation:
Department of Mathematics, Centre for Advanced Study in Mathematics, Panjab University, Chandigarh 160014, India.
M.K. Agrawal
Affiliation:
Department of Mathematics, Centre for Advanced Study in Mathematics, Panjab University, Chandigarh 160014, India.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The statement 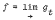used in proving Theorem 2 of [1] needs explanation. This was pointed out to us by Professor S. Raghwan of Tata Institute of Fundamental Research, Bombay, and we gave the explanation of this in [2]. For the sake of completeness we give here the full proof of the theorem; filling the gap in the proof. We use the same notations and definitions as those of [1]. Also for simplicity of notation we write kmn, gmn and amn to mean km,n, gm,n and a respectively. We need the following lemma.

Type
Addendum
Information
Bulletin of the Australian Mathematical Society , Volume 25 , Issue 3 , June 1982 , pp. 475 - 479
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Aggarwal, A.R. and Agrawal, M.K., “On vector spaces of certain modular forms of given weights”, Bull. Austral. Math. Soc. 16 (1977), 371–378.CrossRefGoogle Scholar
[2]Ram, Agya, “On p-adic modular forms and p-adic zeta functions” (PhD thesis, Panjab University, Chandigarh, India, 1979).Google Scholar