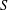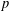Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yu, H.
2017.
On S-semipermutable or S-permutably embedded subgroups of finite groups.
Acta Mathematica Hungarica,
Vol. 151,
Issue. 1,
p.
173.
Qiu, Z.
Chen, G.
and
Liu, J.
2023.
Finite Groups with Some $ S $-Permutably Embedded Subgroups.
Siberian Mathematical Journal,
Vol. 64,
Issue. 4,
p.
1043.
Yu, Haoran
Sun, Jian
and
Guo, Yifan
2023.
A note on a result of Aseeri and Kaspczyk about p-supersolvability of finite groups.
Communications in Algebra,
Vol. 51,
Issue. 11,
p.
4767.
Yu, Haoran
Xu, Xiaowei
and
Zhang, Guanghao
2024.
A note on S-semipermutable and S-permutably embedded subgroups of finite groups.
Ricerche di Matematica,
Vol. 73,
Issue. 4,
p.
2233.