Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T03:23:59.975Z Has data issue: false hasContentIssue false
  • English
  • Français

PERFECT POWERS IN PRODUCTS OF TERMS OF ELLIPTIC DIVISIBILITY SEQUENCES

Part of: Diophantine equations Sequences and sets

Published online by Cambridge University Press:  21 July 2016

LAJOS HAJDU ,
SHANTA LAISHRAM  and
MÁRTON SZIKSZAI
LAJOS HAJDU
Affiliation:
Institute of Mathematics, University of Debrecen, P.O. Box 400, H-4002 Debrecen, Hungary email hajdul@science.unideb.hu
SHANTA LAISHRAM
Affiliation:
Stat-Math Unit, Indian Statistical Institute, 7, S. J. S. Sansanwal Marg, New Delhi, 110016, India email shanta@isid.ac.in
MÁRTON SZIKSZAI*
Affiliation:
Institute of Mathematics, University of Debrecen, P.O. Box 400, H-4002 Debrecen, Hungary email szikszai.marton@science.unideb.hu
*
✉szikszai.marton@science.unideb.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Diophantine problems involving recurrence sequences have a long history. We consider the equation 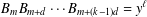$B_{m}B_{m+d}\cdots B_{m+(k-1)d}=y^{\ell }$ in positive integers 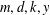$m,d,k,y$ with 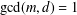$\gcd (m,d)=1$ and 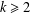$k\geq 2$, where 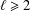$\ell \geq 2$ is a fixed integer and 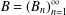$B=(B_{n})_{n=1}^{\infty }$ is an elliptic divisibility sequence, an important class of nonlinear recurrences. We prove that the equation admits only finitely many solutions. In fact, we present an algorithm to find all possible solutions, provided that the set of 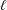$\ell$th powers in 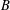$B$ is given. We illustrate our method by an example.

Keywords

perfect powers in productselliptic divisibility sequence

MSC classification

Primary: 11D99: None of the above, but in this section
Secondary: 11B37: Recurrences
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 395 - 404
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Bizim, O. and Gezer, B., ‘Squares in elliptic divisibility sequences’, Acta Arith. 144 (2010), 125–134.Google Scholar
Bizim, O. and Gezer, B., ‘Cubes in elliptic divisibility sequences’, Math. Rep. (Bucur.) 14 (2012), 21–29.Google Scholar
Bravo, J. J., Das, P., Guzmán, S. and Laishram, S., ‘Powers in products of terms of Pell’s and Pell–Lucas Sequences’, Int. J. Number Theory 11 (2015), 1259–1274.CrossRefGoogle Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers’, Ann. of Math. (2) 163 (2006), 969–1018.CrossRefGoogle Scholar
Everest, G., Reynolds, J. and Stevens, S., ‘On the denominators of rational points on elliptic curves’, Bull. Lond. Math. Soc. 39(5) (2007), 762–770.CrossRefGoogle Scholar
Hajdu, L. and Saradha, N., ‘On a problem of Pillai and its generalizations’, Acta Arith. 144 (2010), 323–347.Google Scholar
Hajdu, L. and Szikszai, M., ‘On the GCD-s of k consecutive terms of Lucas sequences’, J. Number Theory 132 (2012), 3056–3069.CrossRefGoogle Scholar
Hajdu, L. and Szikszai, M., ‘On common factors within a series of consecutive terms of an elliptic divisibility sequence’, Publ. Math. Debrecen 84(1–2) (2014), 291–301.CrossRefGoogle Scholar
Laishram, S. and Shorey, T. N., ‘Number of prime divisors in a product of terms of an arithmetic progression’, Indag. Math. (N.S.) 15(4) (2004), 505–521.Google Scholar
Laishram, S. and Shorey, T. N., ‘Number of prime divisors of a product of consecutive integers’, Acta Arith. 113 (2004), 327–341.CrossRefGoogle Scholar
Luca, F. and Shorey, T. N., ‘Diophantine equations with products of consecutive terms in Lucas sequences’, J. Number Theory 114 (2005), 298–311.CrossRefGoogle Scholar
Pethő, A., ‘Perfect powers in second order linear recurrences’, J. Number Theory 15 (1982), 5–13.Google Scholar
Pillai, S. S., ‘On M consecutive integers - I’, Proc. Indian Acad. Sci., Sect. A 11 (1940), 6–12.Google Scholar
Poonen, B., ‘Using elliptic curves of rank one towards the undecidability of Hilbert’s tenth problem over rings of algebraic integers’, in: Algorithmic Number Theory (Sydney, 2002), Lecture Notes in Computational Science, 2369 (Springer, Berlin, 2002), 33–42.CrossRefGoogle Scholar
Reynolds, J., ‘Perfect powers in elliptic divisibility sequences’, J. Number Theory 132 (2012), 998–1015.Google Scholar
Rosser, J. B. and Schoenfeld, L., ‘Approximate formulas for some functions of prime numbers’, Illinois J. Math. 6 (1962), 64–94.Google Scholar
Shipsey, R., Elliptic Divisibility Sequences. PhD Thesis, Goldsmiths College, University of London. 2000.Google Scholar
Shorey, T. N. and Stewart, C. L., ‘Pure powers in recurrence sequences and some related Diophantine equations’, J. Number Theory 27 (1987), 324–352.Google Scholar
Shorey, T. N. and Tijdeman, R., Exponential Diophantine Equations (Cambridge University Press, Cambridge, 1986).Google Scholar
Silverman, J. H., ‘Wiefrich’s criterion and the abc-conjecture’, J. Number Theory 30 (1988), 226–237.CrossRefGoogle Scholar
Stange, K., ‘The Tate pairing via elliptic nets’, in: Pairing-Based Cryptography (Tokyo, 2007), Lecture Notes in Computational Science, 4575 (Springer, Berlin, 2007), 329–348.Google Scholar
Swart, C. S., Elliptic Divisibility Sequences. PhD Thesis, Royal Holloway, University of London. 2003.Google Scholar
Ward, M., ‘Memoir on elliptic divisibility sequences’, Amer. J. Math. 70 (1948), 31–74.Google Scholar